slama.dev

A Chess Engine, Commit by Commit

7. 10. 2025 · [edit]

• Move Generation
  • Bitboards
  • Perft tests
  • Magic bitboards
  • Zobrist hashing
  • Pins via Magic Bitboards
  • Legal Move Generation
  • Const Generics
  • Summary
• Search & Evaluation
  • Alpha-Beta Search
  • Material Evaluation
  • Piece-Square Tables
  • Move Ordering
  • Quiescence Search
  • Transposition Table
  • Killer Moves
  • Delta Pruning
  • Null Move Pruning
  • Late Move Reduction
  • Aspiration Windows
  • Summary
• Resources

Prokop, a ginger and a friend of mine (these are the same person, which is surprising) recently challenged me to a chess engine duel, which consisted of making a chess engine from scratch and then dueling to see whose is better. Naturally, I agreed. And thus Prokopakop (literally translates to the one that kicked Prokop) was born.

It (unsurprisingly) turns out that there are a lot of things that go into making a chess engine, and I thought it would be interesting to cover my journey of writing the bot in the commits that I made, since they correspond to the order in which I learned the various techniques and algorithms that a chess engine uses.

While this article is intended to be read top-to-bottom for beginners to chess-bot-related things, I’ve also added headings for specific topics so that people who are only interested in those can skip around – all sections are self-sustained (as much as they can be), so skipping around is very much encouraged.

If you’d like to play it, you can challenge it on Lichess; just keep in mind that it won’t play more than one game at a time, because the server it’s running on only has two cores, and using both would take this website down.

Finally, I assume that you know chess rules, because you managed to stumble upon this exceedingly nerdy post about a chess engine and have read this far. If not, this will be a wild ride. 🕊

a1f8b8

Move Generation

Before beginning to write a chess bot that searches/evaluates positions, we need to make sure that we can generate them quickly. If you’re not too interested in how the positions are generated (which is a red flag, since I’d say that this is the more interesting part), you can skip to the search & evaluation portion of the article.

The first commit actually contains quite a bit of code, and should have likely been split into separate ones. However, I wanted the first commit to actually contain something that remotely resembles a chess engine, so here we are.

Bitboards

The most important part of this commit is that it stores the board state position via bitboards, which are necessary for making the engine fast. The concept is very simple – since CPUs are heavily optimized for working with 64-bit numbers, and 64 turns out to be the exact number of squares on the board, we can use them to store (among other things) locations of pieces!

As an example, here is a bitboard (=64-bit unsigned integer) that stores pawn positions.

0b00000000⏎     8 ........
  11111111⏎     7 ♙♙♙♙♙♙♙♙
  00000000⏎     6 ........
  00000000⏎     5 ........
  00000000⏎  →  4 ........
  00000000⏎     3 ........
  11111111⏎     2 ♟♟♟♟♟♟♟♟
  00000000      1 ........
                  abcdefgh

The main advantage of storing information in 64-bit numbers is that we can combine multiple bitboards using binary operations to obtain a particular set of squares we need. Prokopakop stores them in the following way:

pub type Bitboard = u64;

pub enum Piece {
    Rook = 0,
    Bishop = 1,
    Queen = 2,
    Knight = 3,
    Pawn = 4,
    King = 5,
}

pub enum Color {
    Black = 0,
    White = 1,
}

pub struct Game {
    // two bitboards for black/white pieces
    pub color_bb: [Bitboard; Color::COUNT],

    // six bitboards for piece types
    pub piece_bb: [Bitboard; Piece::COUNT],

    // ...
}

As an example, to obtain all positions of white rooks and bishops, all we need to¹ do is

self.color_bb[Color::White] & ( self.piece_bb[Piece::Rook]
                              | self.piece_bb[Piece::Bishop]);

There will be plenty more bitboard magic in the following commits, but this will do for now.

Perft tests

To ensure that the chess engine is generating the correct moves, this commit also sets up tests for checking perft (short for performance test), which checks how many legal moves there are up until the given depth. For example

• perft(1) = 20 – there are $8 \cdot 2$ white pawn moves and $4$ knight moves
• perft(2) = 400 – for each perft(1) position, there are 20 moves for black

I’ve borrowed a large perft table from Vajolet, a fellow chess engine, because testing perft for only the starting position won’t help with debugging most of the trickier chess rules. This is especially true in the beginning, when the engine is also very slow and can’t get to the tricky positions too quickly.

6ddcef~67d0e6

This commit adds pre-computing of the possible moves/attacks for pieces at compile time, which means that we can easily obtain squares for all pieces by simply accessing a table. This notably doesn’t work for sliding pieces (rook, bishop, queen), because they can be blocked by other pieces… but that is a problem for a future commit.

It also added en-passant functionality, for which we’ll add

pub struct Game {
    // ...

    // if a pawn just moved two squares,
    // 1 will be at the square over which it moved
    en_passant_bitmap: Bitboard,

    // ...
}

Although this is a bit wasteful since we could just store the column (chess people call them files, but I’m not falling for the propaganda), but having a bitmap is nice since we can more easily check if a pawn can “capture” that square.

178193

Magic bitboards

As I’ve previously mentioned, calculating legal moves for slider pieces can be tricky, because they can be blocked. It would be great if we could pre-compute moves for all possible combinations of blockers, since we’d otherwise have to “raycast” from each slider until we hit a piece, which is slow.

As an example, a rook on d5 with the following configuration of blockers should produce the following bitboard of moves + attacks (from now on, I’m leaving out the 0b and ⏎, but any zeros/ones in an 8x8 shape are still u64):

8 ...♙....     00000000
7 ........     00000000
6 ...♙....     00010000
5 ♙--♜-♙..     11101100
4 ...|....  →  00010000
3 ...|....     00010000
2 ...♙....     00010000
1 ........     00000000
  abcdefgh

The reason why we can’t precompute the moves naively is that we’d either have to use a hashmap of blocker_state → bitboard, which will be much slower than the raycasting approach, or create an enormous array of size $2^{64}$ to use the blocker state as the index, in which case we’d need about 128 exabytes of memory, which I currently do not possess.

Magic bitboards solve this problem in a rather elegant way – notice that in our example, we actually only care about a portion of the squares (in this case the row + column the rook is in), since these are the only squares where placing blockers would limit the rook movement. The issue is that they are scattered all over the bitboard – if they were consecutive, we could use them for indexing… so we’ll create this mapping!

To do this, we will, for each square, generate a magic number that, when multiplying the blocker bitmap, does exactly what we want – it maps the bits we care about to a combination of consecutive positions to be used for indexing, as seen in the following diagram:

bits we       cool         bits
care      *   magic     =  we care
about         number       about,
                           together

........      10001110     17482605
...0....      01011010     39......
...1....      00000110     ........
.23♜456.      01000000     ........
...7....  *   11001101  =  ........
...8....      00000001     ........
...9....      10111111     ........
........      00100111     ........

Finally, we shift right to obtain only the bits we care about, obtaining the key we will use to access the precomputed array of rook/bishop moves. This is the reason for why we’d like the consecutive positions to start from the most significant bits – that way a single shr operation is enough to obtain the index (otherwise we’d need two shifts, or some masking).

( bits we       cool   )      (64 - num)     key for
( care      *   magic  )  >>  (of bits )  =  indexing
( about         number )      (together)     the array


(........      10001110)                     ........
(...0....      01011010)                     ........
(...1....      00000110)                     ........
(.23♜456.      01000000)                     ........
(...7....  *   11001101)  >>  (64 - 10)   =  ........
(...8....      00000001)                     ........
(...9....      10111111)                     ......17
(........      00100111)                     48260539

Putting this together, we can now retrieve the slider move bitboards by using two arrays – an array to store the magic numbers + number of bits they map to + offsets to the main array where moves for that square start, and the main array storing the actual move bitboards.

In practice, magic numbers can be generated rather quickly by trying random numbers (those with a low number of non-zero bits work the best), and either loaded from a file, or compiled in.

037103~33cbd8

Adds the remaining chess rules, making the engine an actual engine for the first time as the perft tests are finally passing! This includes:

• promotion (implemented twice; the first implementation let you promote to a king),
• history, so we can undo moves,
• castling, which requires that we keep track of whether we can castle kingside/queenside, and whether the squares over which the king would be moving aren’t under attack, and
• attack bitboard calculation for both colors, which pre-calculates all squares attacked by the opponent (won’t go into detail since they were removed shortly after due to being too slow)

These changes expand our Game struct:

pub struct Game {
    // ...

    // 0x0000KQkq, where kq/KQ is one if black/white king and queen
    castling_flags: u8,

    // store the move, which piece was there, and en-passant + castling flags
    // the flags can NOT be calculated as an arbitrary position can have those
    // (move, captured_piece, castling_flags, en_passant_bitmap)
    pub history: Vec<(BoardMove, Option<ColoredPiece>, u8, Bitboard)>,

    // store the attack bitboards for both colors,
    // with 1 being that some piece attacks the square
    pub attack_bitboards: [Bitboard; Color::COUNT],
}

With all of these chess rules implemented, the moves are generated via the make + unmake approach to move generation – we first generate pseudo-legal moves (moves where the king can come under attack), perform them, check whether the king is actually under attack, and if not, this move is legal.

We’ll replace this with legal-move generation later later, since it’s much faster.

dc9fc0

Zobrist hashing

When doing search over chess positions, knowing which we’ve already seen (and can thus skip since we’ve evaluated it already) is crucial for making a chess engine fast. We would like to be able to map board_state → arbitrary_data, but how do we find a suitable key?

To uniquely² identify a chess position, we store

• $64b$ for piece colors + ${\sim}3b * 64$ for piece types,
• $64b$ for en-passant bitmap,
• $4b \cdot 2$ for castling information,
• $1b$ for whose turn it is,

which is too many to use as a key for a hash table, if we want it to be fast. Ideally, we’d like to reduce those to 64, which is much nicer to work with while still having a low chance of collision³ over the runtime of a standard chess game.

Zobrist hashing does this in a rather simple way – we generate random numbers for all of the things mentioned above, and XOR all that apply (with an additional one for en-passant⁴) to create the game identifier:

struct ZobristKeys {
    // every combination of color-piece-square
    pub pieces: [[[u64; 64]; Piece::COUNT]; Color::COUNT],

    // every combination of the 4 castling bits
    pub castling: [u64; 16],

    // every en-passant column; see footnote for explanation of +1
    pub en_passant: [u64; 8 + 1],

    // is it black's turn?
    pub side_to_move: u64,
}

Since XOR is commutative, we can iteratively update the current hash after every move by XORing only the things that actually changed, which adds very little overhead.

I’ve also added Zobrist hashing to the current perft implementation, since that is a great way to test whether it works as it should. Generally, we should only do this once the tests are passing without hashing, otherwise the debugging will be miserable (speaking from personal experience).

a6156e~f0253e

Removes attack bitboards in favor of simply checking whether any pieces are attacking a particular square, since most code doesn’t need them anyway, but they needed to be recalculated after each move. Also does a bit of refactoring, but nothing too exciting.

d7c5b4

Compacts a board move to $16$ bits – $5 * 2$ for source + destination square indexes, and $4$ for identifying a promotion piece (if applicable). Might not seem like a big change, but board moves are used ubiquitously though the engine, so making them as compact as possible while not sacrificing too much speed is generally a good idea.

dda91d

Pins via Magic Bitboards

When a piece is pinned, we need to limit its movement along the ray of the pin (i.e. between the attacker and the king). We can obviously do this by “raycasting” (i.e. iterating from the king square), but that is boring and slow. Instead, we can use a trick – since we’ve already implemented magic bitboards, we can use them by pretending that the king is a queen, getting candidate blockers (white pawns), removing those, and using them again to get the attackers (black rook and bishop).

  magic bb       remove         magic bb
  to get         the hit        to get
  blockers       pieces         pinners

8 ........     8 ........     8 ........
7 .....♖..     7 .....♖..     7 .....♖..
6 .♗......     6 .♗......     6 .♗...|..
5 .....♟..     5 .....x..     5 ..\..|..
4 ...♟.|./  →  4 ...x....  →  4 ...\.|./
3 ....\|/.     3 ........     3 ....\|/.
2 -----♚--     2 .....♚..     2 -----♚--
1 ..../|\.     1 ........     1 ..../|\.
  abcdefgh       abcdefgh       abcdefgh

There is a slight catch: to obtain the positions of the blockers, we need either a third magic bitboard access from the position of the blocker, or use precomputed rays between squares; I haven’t been able to find a smarter way to do this, please let me know if there is one.

896a48~5bc16a

Legal Move Generation

As we’ve already discussed, we are currently generating legal moves by first generating all pseudo-legal moves (those where king can be under attack afterwards), making them, checking whether the king is in check afterwards, and finally unmaking them.

A faster approach is to generate legal moves directly, without having to modify the board state. This, however, is much more complicated, as the king can come under attack in a number of tricky ways (most of which having to do with en-passant; curse the French!). In Prokopakop, I distinguish between three cases, depending on the number of attacks the king is under:

• 0 attacks: normal generation; just watch for pins
• 1 attack: king has to either move away, or the attacker must be captured; also watch for pins
• 2 attacks+: king can only move away

Separating the cases makes legal move generation more manageable, and makes it much faster than make/unmake-based move generation. Instead of going through the code (which, if you’re interested, can be found here), I’ll point you towards Peter Ellis Jones’ excellent blog post on legal move generation, as it was a great resource when implementing it myself.

990204~3ff11a

Const Generics

Besides small improvements/optimizations, the main change that I made was to replace most of the move generation code by const generic variants. This is just a fancy way of saying that most functions in my code have multiple variants for pieces/colors, which reduces the number of branches in the code and thus speeds it up.

It’s important to note here that we’re not talking about runtime variants, where a function takes a Piece and does different things depending on which piece it is. In our case, this happens at compile-time – instead of make_move(piece, ...), we have make_rook_move(...) (as well as all other pieces).

As an example, the outer if in this code:

// update castling rights when rook moves
if P::PIECE == Piece::Rook {
    let castling_flags = self.castling_flags
        & !match (C::COLOR, board_move.get_from()) {
            (Color::Black, BoardSquare::H8) => 0b00000001,
            (Color::Black, BoardSquare::A8) => 0b00000010,
            (Color::White, BoardSquare::H1) => 0b00000100,
            (Color::White, BoardSquare::A1) => 0b00001000,
            _ => 0,
        };

    self.update_castling_flags(castling_flags);
}

gets evaluated at compile time, so all of this code will only be included in the rook version of the function. No branching, no problem!

Summary

As we have reached the end of the move generation portion of this article, here is the speed of move generation across the commits that we’ve discussed (benchmarked via hyperfine, with hashing enabled).

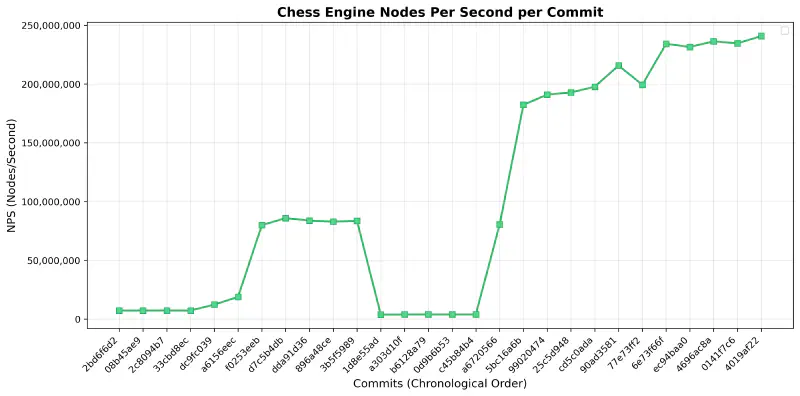
As we can see, three places stand out in this graph:

• the first major spike in speed (commit f0253e) was caused by removing the attack bitboards; since these were previously calculated every move and consisted of evaluating all attacks of all pieces on the board, this is not surprising
• the first major crash (commit 1d8e55) was caused by starting to move away from the make/unmake-based move generation by splitting each move generation into different functions based on the number of attacks; as this only included the spitting, but no optimized code, this introduced a large amount of branching that killed the speed
• the second major spike (commits a67205 and 5bc16a) were caused by finishing moving away from the make/unmake-free move generation by introducing functions optimized for zero/one/two+ king attacks

The engine is slower than Stockfish ($9.74\text{s}$ for Prokopakop vs. $8.71\text{s}$ for Stockfish on perft(7)), but this is simply a skill issue because I’m not spending more time on this when I haven’t written any search & evaluation functionality yet. Maybe I’ll revisit to take my revenge on Stockfish at some point in the future, but this will have to do for now.

Search & Evaluation

Now that we can generate moves quickly (for some definition of quickly), we need to search through them to find the best one and evaluate the resulting positions. Since chess is a zero-sum two-player game, we can simply assign each position a score (white is positive, black is negative) based on things like piece positions, counts, etc., and always pick the move that leads to the best score for the moving player.

                     Current
                   (Max: +0.8)
                        │
       ┌────────────────┼────────────────┐   maximizing
       ↓                │                │
    Move A           Move B           Move C
   (Normal)        (Queen Sac)      (Pawn Sack)
  (Min: +0.8)      (Min: -7.2)      (Min: -0.7)
       │                │                │
       │                │                │
  ┌────┼────┐      ┌────┼────┐      ┌────┼────┐   minimizing
  ↓    │    │      │    │    ↓      │    │    ↓
+0.8 +1.2 +0.9   -6.1 -5.8 -7.2   -0.3 +0.1 -0.7

This is called the minimax algorithm, and is at the heart of most⁵ strong chess engines (Prokopakop included). The algorithm works by recursively exploring all possible moves to a certain depth. When it’s our turn (maximizing player), we want to pick the move that leads to the highest score. When it’s the opponent’s turn (minimizing player), they will pick the move that leads to the lowest score (best for them, worst for us).

At each leaf node (when we’ve reached our search depth), we evaluate the position, i.e. how good it is for the player whose turn it is. Then we propagate these scores back up the tree: maximizing nodes take the maximum of their children’s scores, minimizing nodes take the minimum.

9fec3a0

Alpha-Beta Search

While minimax is an important foundation to our search functionality, we can greatly improve it, as the first commit in this part of the article does, by using alpha-beta pruning.

Let’s say that we we have just fully explored the move A, which was a regular move that gave us a slight advantage. We then proceed to B, which is actually a blunder, and we find this out quickly after exploring the first opponent response, which is extremely strong. Since the opponent has a strong response, which if he were to play would put us in a worse position than A, we can prune the rest of B – no matter what the other moves are, if the opponent picks this response, it will be worse for us than the output of A, so we won’t bother exploring just how bad it is for us.

                     Current
                        │
       ┌────────────────┼────────────────┐
       │                │                │
    Move A           Move B           Move C
   (Normal)        (Queen Sac)      (Pawn Sack)
  (Min: +0.8)     (Min <= -6.1)
       │                │
       │                │
  ┌────┼────┐      ┌────┼────┐
  ↓    │    │      ↓    │    │
+0.8 +1.2 +0.9   -6.1   ?    ?   PRUNED

Formally, we track the best values the players can achieve in the particular position as $\alpha$ (white) and $\beta$ (black), and induce a cutoff if $\beta \le \alpha$ – this is something that can only happen if, at some earlier point of the search tree, we had a better option to pick.

We can see how these values get updated on the example we just covered – first, exploring branch A returns +0.8, which is then used to update $\alpha$. Next, exploration of branch B is started, with the first move returning -6.1, which is then used to update $\beta$. At this point, we can see that $\beta \le \alpha$, so we can prune the rest of the tree.

                     Current
                        │
       ┌────────────────┼────────────────┐
       │                │                │
    Move A           Move B           Move C
   (Normal)        (Queen Sac)      (Pawn Sack)
  α=-∞, β=+∞      α=+0.8, β=+∞
       │                │
       │                │
  ┌────┼────┐      ┌────┼────┐
  ↓    │    │      ↓    │    │
+0.8 +1.2 +0.9   -6.1   ?    ?

                     β <= α
                  -6.1 <= +0.8
                 CUTOFF INDUCED

Prokopakop (and most other engines) implements this via negamax, which simplifies the implementation by always maximizing and flipping + negating the alpha/beta values and evaluation when doing the recursive call, as we’re changing perspectives. This is very convenient, because it simplifies both the implementation and the conceptual meaning of alpha and beta – we can now always think of alpha as the lower bound (what we are guaranteed somewhere in the search tree), and beta as the upper bound (what the opponent won’t allow us to exceed because of what he has guaranteed somewhere in the search tree).

This commit also implements iterative deepening for time management, which runs alpha-beta search with depths $1, 2, \ldots$ until time runs out and returns the best result found, so we can limit time spent on searching based on the current time control.

Note that for alpha-beta search to work well, we need to ensure that the moves are ordered from strongest to the weakest, as exploring more interesting lines first will induce more cutoffs, as compared to when the moves are unordered – we’ll implement this later.

Material Evaluation

As a final step in this initial search/eval commit, we implement a basic evaluation function, which simply counts material. While this might seem like all we need, this is generally not sufficient as it doesn’t take into account many nuances of the position, such as pawn structure, piece mobility, etc. We’ll improve this in the very next commit.

8eeb84e~6aec863

Piece-Square Tables

This commit adds piece-square tables for positional evaluation. These are a set of tables that, for each piece, provide information about how much it is worth when being on a particular square. As an example, here is a pawn table:

const PAWN_TABLE: [f32; 64] = [
    0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  0.0,
   +1.0, +1.0, +1.0, +1.0, +1.0, +1.0, +1.0, +1.0,
   +0.2, +0.2, +0.4, +0.6, +0.6, +0.4, +0.2, +0.2,
   +0.1, +0.1, +0.2, +0.5, +0.5, +0.2, +0.1, +0.1,
    0.0,  0.0,  0.0, +0.4, +0.4,  0.0,  0.0,  0.0,
   +0.1, -0.1, -0.2,  0.0,  0.0, -0.2, -0.1, +0.1,
   +0.1, +0.2, +0.2, -0.4, -0.4, +0.2, +0.2, +0.1,
    0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  0.0,  0.0,
];

Positive values correspond to places where pawns are more valuable, while negative values correspond to those where they are less valuable. For pawns, these values try to incentivize center pawn pushes and promotions, and discourage advancing pawns that shield the king.

For certain pieces, we can take this one step further and have two tables – one for “early” game and one for “late” game (for some suitable definitions of early and late, such as total remaining material), and interpolate between them based on the current game phase. This is typically done for the king, as we want him to be more protected in the early game, and more aggressive in the late game:

const KING_EARLY_TABLE: [f32; 64] = [
   +0.2, +0.1, +0.1,  0.0,  0.0, +0.1, +0.1, +0.2,
   +0.2, +0.1, +0.1,  0.0,  0.0, +0.1, +0.1, +0.2,
   +0.2, +0.1, +0.1,  0.0,  0.0, +0.1, +0.1, +0.2,
   +0.2, +0.1, +0.1,  0.0,  0.0, +0.1, +0.1, +0.2,
   +0.3, +0.2, +0.2, +0.1, +0.1, +0.2, +0.2, +0.3,
   +0.4, +0.3, +0.3, +0.3, +0.3, +0.3, +0.3, +0.4,
   +0.7, +0.7, +0.5, +0.5, +0.5, +0.5, +0.7, +0.7,
   +0.7, +0.7, +1.0, +0.5, +0.5, +0.6, +1.0, +0.7,
];

const KING_LATE_TABLE: [f32; 64] = [
    0.0, +0.1, +0.2, +0.3, +0.3, +0.2, +0.1,  0.0,
   +0.2, +0.3, +0.4, +0.5, +0.5, +0.4, +0.3, +0.2,
   +0.2, +0.4, +0.7, +0.8, +0.8, +0.7, +0.4, +0.2,
   +0.2, +0.4, +0.8, +0.9, +0.9, +0.8, +0.4, +0.2,
   +0.2, +0.4, +0.8, +0.9, +0.9, +0.8, +0.4, +0.2,
   +0.2, +0.4, +0.7, +0.8, +0.8, +0.7, +0.4, +0.2,
   +0.2, +0.2, +0.5, +0.5, +0.5, +0.5, +0.2, +0.2,
    0.0, +0.2, +0.2, +0.2, +0.2, +0.2, +0.2,  0.0,
];

53a09e5

Move Ordering

As mentioned in the alpha-beta section, for the moves to be pruned efficiently, we need to pick the strongest moves early so that they can be searched first and used for pruning the later branches. While this is quite difficult to do in general, we can use heuristics that perform well in practice. The most straightforward one is for ordering capturing moves, and it is exactly what you’re thinking of – capture the most valuable victim with the least valuable attacker (MVV-LVA).

This, combined with always searching the moves from the principal variation first (best line found in the previous iteration of iterative deepening), gives a decent ordering and provides a good speed-up to the alpha-beta search.

bbef3be

Quiescence Search

Using alpha-beta search with iterative deepening means that we always, for depths $1, \ldots, n$, explore until a certain depth and then evaluate the position. This has an obvious flaw: what if we make blunder, like taking a queen for a pawn, in the final depth? Since this was the last depth that we were searching, this wouldn’t get caught, and we’d happily return positive evaluation, since we’re up a pawn!

This is where quiescence search⁶ comes in – when reaching the final depth of the iteration, it extends the search until all remaining captures (and possibly checks) are resolved, so that we are only evaluating quiet positions (i.e. those where there are no tactical sequences that can severely impact the score). This way, we don’t make obvious blunders because of a search cut short.

35f6fb6

Transposition Table

Re-evaluating a position we have already reached and evaluated would be a waste, so let’s not do that and implement a transposition table (TT). Since we’ve already implemented zobrist hashing, we can quickly identify explored positions and avoid needless computation… but what do we actually store?

Let’s look at a minimax search first – when evaluating a position, we examine all moves until a certain depth, so the calculated evaluation is exact up until the given depth. When reaching this position again, we can use this already calculated value if the depth we’re searching to is less than or equal to the one we already did. Conversely, if the depth we’re searching to exceeds the one we already explored, we need to actually do the computation.

Alpha-beta makes this slightly more difficult, because we’re not exploring the entire tree. This means that while we sometimes only get bounds on the evaluation, this is still useful information. We distinguish two new cases:

1. If we prune a branch (i.e. cause a beta cut-off), it is because we found a move that is too good and the other player won’t allow us to play it because they’ll play something elsewhere in the tree (the move fails high). This means that the evaluation of this branch can only get better for us as we go through the moves, so we get a lower bound (/).
2. If we, on the other hand, go through all moves and none of them improve alpha (the move fails low), it means that the position can’t score better than what we have found, and we have thus found an upper bound.

Adding these two cases, we store three types of nodes – exact, lower bound and upper bound. Implementation-wise, we’d store something like this:

pub enum NodeType {
    Exact,
    LowerBound,
    UpperBound,
}

pub struct TTEntry {
    pub key: u64,             // zobrist hash
    pub depth: u8,            // how far we searched
    pub evaluation: f32,      // evaluation of this branch
    pub node_type: NodeType,  // what type of information we obtained

    // These are not required, but useful
    pub best_move: Move,      // best move found
    pub age: u8,              // age of this entry, so we can clear the old ones
}

For implementing the TT itself, we can use a nice trick: instead of using a hashmap, use a fixed array of size $2^n$ and the first $\mathbf{n}$ bits of the zobrist hash as an index… because why would we hash twice?

There are many other things to consider like replacement strategies and more advanced TT implementations, such as using buckets, but I won’t go into detail on those as we’ve covered the core concepts behind TTs.

A small terminology note: when doing research for this article, I found that the three node categories described above are sometimes called PV (exact), Cut (lower bound) and All (upper bound) nodes, so don’t be surprised when you see these terms used; they refer to the node types. This mainly originates from a 2003 paper about pruning methods⁷.

ff14c29~6c4e7ee

I’ve added threefold repetition detection, but only for the first few plys (this is what the chess people call turns, and corresponds to the current depth we’re in⁸), since the check can be rather expensive. In addition, I’ve improved the evaluation function to incentivize passed pawns, penalize doubled pawns, and account for piece mobility by counting moves available to each piece from both sides.

2c1a839

Killer Moves

In certain positions, there are responses that can act as refutations to multiple moves that the opponent might like to play. As an example, if pushing a pawn kicks out an annoying knight, it can also be a good response to the opponent’s other moves, like blocking a bishop, threatening a pushed pawn, etc…

More specifically: if a move causes a beta cut-off, it means that it’s likely a good response and should be prioritized in sibling branches. To do this, we remember it for this ply and prioritize it in move order. Since we already have MVV-LVA, which handles capture ordering well, we will only do this for non-capture (i.e. quiet) moves.

In practice, it is usually better to store two moves for each ply, because there can be cutoffs that are not really killer and could mess with the move ordering. The implementation itself is very easy (with suitable updates as we traverse the search tree):

pub struct KillerMoves {
    // 2 killer moves per ply
    killers: Vec<[BoardMove; 2]>,
}

a28d291

Delta Pruning

Up until now, all of the things⁹ that we implemented were a part of the classical alpha-beta algorithm, which means that the calculated score for the given depth was exact… but that’s still too slow for us. Let’s start cutting corners 😎.

We’ll begin by implementing delta pruning for quiescence search. It’s a rather intuitive heuristic on whether we should explore a particular move – if capturing the piece + some safety margin (usually two pawns), is not sufficient to raise alpha, then we don’t bother exploring the move at all since we are, as the kids say, beyond cooked and the position is hopeless.

While this will speed up the search because we’re no longer exploring likely hopeless positions, we can miss certain tactical sequences, especially those that swing the evaluation by more than the safety margin (since that’s the maximum we’re assuming we could gain). It is therefore recommended to not use this heuristic when approaching the endgame, because we might need to sacrifice some material for positional advantage and conversion.

Techniques that prune branches with the risk of overlooking things are referred to as forward pruning, and we’ll be implementing a lot more of them in the next few commits, since we’ve mostly run out of the regular (sometimes called “backward”) pruning techniques that keep the evaluation exact.

10c64e9

Null Move Pruning

Let’s cut the corners even further!

Null move pruning uses the simple observation that skipping a turn (i.e. making a null move) is almost¹⁰ always worse than making the best move in the position. Therefore, it’s a relatively safe assumption that if making a null move causes a beta cut-off (i.e. even not making any move is so good and the opponent wouldn’t let us play it), we can prune this entire branch without exploring any of the moves, since the best move is bound to be better than no move at all.

Implementation-wise, two things to mention:

• The search on the null move uses a reduced depth (either flat or progressive), because it should usually be apparent quite quickly whether a beta cut-off will occur or not.
• If the evaluation of the current position is below beta (with some margin), we don’t need to try null move pruning, since it extremely unlikely to result in a beta cut-off anyway.

5047857

Late Move Reduction

The shape of our engine is still not spherical enough – more corner cutting!

With move ordering implemented (MVV-LVA, principal variation, killer moves and transposition table), we usually have a good idea on which moves look promising, and we explore those first to induce as many cut-offs as possible. It therefore stands to reason that quiet moves that come later in the move order (hence the name late move reduction) are not that interesting.

To not waste time, we explore them with a reduced depth and distinguish two cases:

• If they don’t improve alpha (fail low), we were right – they are not interesting and we do not explore them further.
• If, on the other hand, they do exceed alpha, we need to re-run the search with the original depth, since we don’t want to miss a potentially interesting line.

Take note that in this case, we don’t care about beta when checking the result of the reduced search, since we’re expecting the moves to be bad anyway – we only care about checking that they’re worse than alpha and so not worth consideration.

da6dbb0

Aspiration Windows

When doing iterative deepening, each successive iteration returns an evaluation of the position. If we have a well-behaved alpha-beta implementation and evaluation function, the evaluation will not swing wildly as the search goes on, but instead stabilize around some “true” evaluation of the position.

Aspiration window search takes advantage of this observation by setting the alpha and beta bounds in alpha-beta search to the previous iterative deepening iteration result $\pm$ some margin (usually half a pawn).

Running this search, two things can happen with the root result:

• The evaluation is within the bounds of the aspiration window, which means we were correct and this is the true evaluation. Yippie!
• The evaluation is outside the bounds (either fail low or fail high), which means that the guess was wrong; in that case we need to re-search with a larger window (usually extending the side of the bound that failed), until the search succeeds. Boo!

Aspiration windows were difficult for me to understand initially, so here is the observation that made it click: if the value calculated from alpha-beta search falls within the alpha-beta bounds, then it is exact. This is because we found a line that leads to a position with the expected evaluation, and there is no line that is better/worse than the provided bounds.

If we misjudge the position, and there is a line outside of this evaluation, then this will lead to a fail (low or high) and the aspiration window search will return only a bound – since we don’t know what the actual value is, we have to re-run.

To be continued?

Summary

I’ll end the article here (at least for now), since I’m still actively developing the engine, so waiting until it’s complete would likely mean that I would take this to my grave. If people find this interesting, I’ll keep updating it as more commits come in, but this is definitely more than enough to write an engine that will beat most chess players with relative ease.

Here is a table of engine performance across different versions (100 games between each pair), using fastchess to facilitate the matches via the UCI protocol that the engine implements. The named versions are commits implementing things we described in the article, while master (~2000 on Lichess) is the latest version that contains a bunch more that I couldn’t cover.

Name            nElo      +/-    Score     Draw                   Ptnml(0-2)
----            ----      ---    -----     ----                   ----------
master       +420.38    21.53    84.0%     9.2%    [  1,  16,  46, 177, 260]
1fb64eb-4    +123.74    21.53    67.1%    18.8%    [ 48,  61,  94,  95, 202]
10c64e9-3     +31.00    21.53    54.5%    23.6%    [ 86,  86, 118,  71, 139]
2c1a839-2     -12.60    21.53    48.2%    31.4%    [124,  49, 157,  79,  91]
6c4e7ee-1     -88.68    21.53    37.5%    25.4%    [162, 108, 127,  25,  78]
bbef3be-0    -708.33    21.53     8.8%     4.4%    [349, 128,  22,   1,   0]

In the table, Ptnml(0-2) is short for pentanomial model, which is used to evaluate the engine performances. Engines are repeatedly played against each other for random opening positions, and in each case play two games (one with white, one with black). The results are then [ll, dl, dd/wl, wd, ww] for win, draw and loss respectively, which is better for measuring the performances than a simple win/draw/loss ratio, especially for uneven positions

That’s it. Thanks for reading! ❤️

Resources

• Chess Programming Wiki – an extremely well-written wiki that I took the vast majority of algorithms and techniques from.
• Peter Ellis Jones’ blog post about legal move generation helped me debug a number of tricky situations (cough en-passant cough).
• fastchess and hyperfine for benchmarking the movegen + play.
• Lichess and their plug-and-play bot bridge, making it possible to play the bot online.

Special thanks to Prokop for the original nerdsnipe and proofreading.