Camera and Graphs

Manim · 3. 7. 2022 · Part 1, Part 2, → Part 3 ←, Part 4, Part 5, Part 6 · [edit]

This part of the series covers mainly two topics – the camera and (combinatorial) graphs. Besides this, it also includes some useful concepts for more advanced animations.

`save` and `restore`

Each Manim object (MObject ) contains the save_state function that allows to save the current state of the object, which it can later go back to using the restore function (possibly using the animate syntax). This makes the code, in certain situations, much more compact and readable.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
from manim import *


class SaveAndRestoreExample(Scene):
    def construct(self):
        square = Square()

        square.save_state()

        self.play(Write(square))

        self.play(square.animate.set_fill(WHITE, 1))
        self.play(square.animate.scale(1.5).rotate(PI / 4))
        self.play(square.animate.set_color(BLUE))

        self.play(square.animate.restore())

        self.play(Unwrite(square))

One animation that we used here but haven’t seen yet is the Unwrite , which is Write in reverse.

Graphs

Introduction

Combinatorial graphs are a necessary component of any mathematical library and Manim is no exception. They are implemented using the Graph class.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from manim import *


class GraphExample(Scene):
    def construct(self):
        # the graph class expects a list of vertices and edges
        vertices = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
        edges = [
            (1, 2),
            (2, 3),
            (3, 4),
            (2, 4),
            (2, 5),
            (6, 5),
            (1, 7),
            (5, 7),
            (2, 8),
            (1, 9),
            (10, 8),
            (5, 11),
        ]

        # we're using the layout_config's seed parameter to deterministically set the
        # vertex positions (it is otherwise set randomly)
        g = Graph(vertices, edges, layout_config={"seed": 0}).scale(1.6)

        self.play(Write(g))

        # the graph contains updaters that align edges with their vertices
        self.play(g.vertices[6].animate.shift((LEFT + DOWN) * 0.5))

        self.play(g.animate.shift(LEFT * 3))

        # the graphs can also contain labels and be organized into specific layouts
        # (see the Graph class documentation for the list of all possible layouts)
        h = Graph(vertices, edges, labels=True, layout="circular").shift(RIGHT * 3)

        self.play(Write(h))

        # color the vertex 5 and all of its neighbours
        v = 5
        self.play(
            Flash(g.vertices[v], color=RED, flash_radius=0.5),
            g.vertices[v].animate.set_color(RED),
            *[g.edges[e].animate.set_color(RED) for e in g.edges if v in e],
        )

As you can see from the code, the Graph expects a list of vertices and edges as the input. To access them, we will use the graph.vertices and graph.edges dictionaries – just be careful that edges of type $(u, v)$ can’t be accessed by using $(v, u)$ (something quite unintuitive for undirected graphs).

The default algorithm for vertex positioning is Fruchterman-Reingold and works in a simple way – vertices have a repulsing force and edges have an attracting one. Besides the seed parameter, the algorithm has a number of other parameters for adjusting its behavior, which you can read about in the link above.

Custom vertices and edges

Note that vertices and edges need not be circles and segments – we can use custom Manim objects and functions for creating more exotic graphs.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from manim import *
from random import uniform, randint, seed


class StarrySkyExample(Scene):
    def construct(self):
        seed(0xDEADBEEF)

        # the graph class expects a list of vertices and edges
        vertices = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
        edges = [
            (1, 2),
            (2, 3),
            (3, 4),
            (2, 4),
            (2, 5),
            (6, 5),
            (1, 7),
            (5, 7),
            (2, 8),
            (1, 9),
            (10, 8),
            (5, 11),
        ]

        def RandomStar():
            """Create a pretty random star."""
            return Star(
                randint(5, 7), fill_opacity=1, outer_radius=0.1, color=WHITE
            ).rotate(uniform(0, 2 * PI))

        def RandomSkyLine(u, v, z_index=None):
            """Create a pretty random sky line. The z_index is necessary, since it is
            passed by the graph constructor to edges so they're behind vertices."""
            return DashedLine(u, v, dash_length=uniform(0.03, 0.07), z_index=z_index)

        # custom graph with star vertices and dashed line edges
        g = (
            Graph(
                vertices,
                edges,
                layout_config={"seed": 0},
                vertex_type=RandomStar,
                edge_type=RandomSkyLine,
            )
            .scale(2)
            .rotate(-PI / 2)
        )

        self.play(Write(g))

        self.play(FadeOut(g))

As the code suggests, the current implementation expects both vertex_type and edge_type to be functions returning a MObject . Besides this, the edge_type function must have an optional z_index parameter, since the graph implementation sets it to a negative number to push the edges behind the vertices. Additionally, the edges must have a put_start_and_end_on function (which DashedLine does), since this is what edge udaters call when vertices move.

Random graphs

If we don’t want to create random graphs manually, we can use the popular networkx library, which contains a number of useful graph generators and graph-related functions.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from manim import *
from random import *
import networkx as nx


class GraphGenerationExample(Scene):
    def construct(self):
        seed(0xDEADBEEF)

        n = 12  # number of vertices
        p = 3 / n  # probability that there is an edge between a pair

        # generate until our graph is not connected (so it looks nicer)
        graph = None
        while graph is None or not nx.is_connected(graph):
            graph = nx.generators.random_graphs.gnp_random_graph(n, p)

        g = (
            Graph.from_networkx(graph, layout_config={"seed": 0})
            .scale(2.2)
            .rotate(-PI / 2)
        )

        self.play(Write(g))

Camera

In Manim, each camera scene contains a camera object (implemented via the Camera ). So far, it wasn’t vert useful, because we’ve implemented all object transformations by changing the objects themselves. In certain cases, however, it is much more convenient to just move/zoom the camera to achieve the same result.

This is not as simple as it seems, because the default Scene class isn’t equipped to deal with a moving camera. That’s why we’ll use the MovingCameraScene , which contains a frame object that we can animate.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from manim import *


class MovingCameraExample(MovingCameraScene):
    def construct(self):
        square = Square()

        self.play(Write(square))

        self.camera.frame.save_state()

        # zoom for the square to fill in the entire view (+ a bit of space)
        self.play(self.camera.frame.animate.set_height(square.height * 1.5))

        circle = Circle().next_to(square, LEFT)

        # move the camera to the new object
        self.play(
            AnimationGroup(
                self.camera.frame.animate.move_to(circle),
                Write(circle),
                lag_ratio=0.5,
            )
        )

        self.wait(0.5)

        # zoom out (increasing frame size covers more of the screen)
        self.play(self.camera.frame.animate.scale(1.3))

        triangle = Triangle().next_to(square, RIGHT)

        # move the camera again
        self.play(
            AnimationGroup(
                self.camera.frame.animate.move_to(triangle),
                Write(triangle),
                lag_ratio=0.5,
            )
        )

        self.wait(0.5)

        self.play(self.camera.frame.animate.restore())

As the example suggests, the self.camera.frame object behaves just like all of the animated objects we’ve seen – we can set its height, scale it, move it, etc. This also means that we can use updaters exactly how one would expect.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from manim import *
from random import *


class MovingCameraUpdaterExample(MovingCameraScene):
    def construct(self):
        seed(0xDEADBEEF)

        n = 11**2

        circles = VGroup(
            *[
                Circle(radius=0.1)
                .scale(uniform(0.5, 2))
                .shift(UP * uniform(-3, 3) + RIGHT * uniform(-5, 5))
                .set_color(WHITE)
                for _ in range(n)
            ]
        )

        # the circle we'll follow
        target = circles[n // 2]

        def follow_camera(camera):
            """An updater that makes sure the camera is on top of the target."""
            camera.move_to(target.get_center())

        self.camera.frame.add_updater(follow_camera)

        # TRIPLE CAUTION!
        # updaters only work on things added to the scene
        # since self.camera.frame is, by default, not on the scene, we need to add it
        self.add(self.camera.frame)

        self.play(FadeIn(circles))

        scale_factor = 0.7

        def arrange_and_zoom(rows, color):
            """Arrange the circles in a grid, zooming the camera in the process."""
            self.play(
                circles.animate.arrange_in_grid(rows=rows).set_color(color),
                self.camera.frame.animate.scale(scale_factor),
                run_time=1.5,
            )

        arrange_and_zoom(7, RED)
        arrange_and_zoom(5, GREEN)
        arrange_and_zoom(14, BLUE)

As the code mentions, it is very important to pay attention to whether the updated object has been added to the scene. In this case, the updater hasn’t been animated yet (which implicitly adds it to the scene), meaning that we had to add it manually.

Besides moving and zooming, we can also do things like changing the color of the background.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
from manim import *


class BackgroundColorExample(MovingCameraScene):
    def construct(self):
        self.camera.background_color = WHITE
        self.camera.frame.scale(0.6)

        square = Square(color=BLACK)

        self.play(Write(square))

        circle = Circle(color=BLACK).next_to(square, LEFT)
        triangle = Triangle(color=BLACK).next_to(square, RIGHT)

        self.play(FadeIn(triangle, shift=RIGHT * 0.2), FadeIn(circle, shift=LEFT * 0.2))

Rate functions

For fine-tuning animations, it is sometimes desirable to change the functions that time them. We’ve already seen

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from manim import *

# shamelessly stolen (modulo minor changes) from the Manim documentation
# https://docs.manim.community/en/stable/reference/manim.utils.rate_functions.html


class RateFunctionsExample(Scene):
    def construct(self):
        line1 = Line(3 * LEFT, RIGHT).set_color(RED)
        line2 = Line(3 * LEFT, RIGHT).set_color(GREEN)
        line3 = Line(3 * LEFT, RIGHT).set_color(BLUE)
        line4 = Line(3 * LEFT, RIGHT).set_color(ORANGE)

        lines = (
            VGroup(line1, line2, line3, line4).arrange(DOWN, buff=0.8).move_to(LEFT * 2)
        )

        dot1 = Dot().move_to(line1.get_start())
        dot2 = Dot().move_to(line2.get_start())
        dot3 = Dot().move_to(line3.get_start())
        dot4 = Dot().move_to(line4.get_start())

        dots = VGroup(dot1, dot2, dot3, dot4)

        # care for writing _ in latex -- needs to be escaped
        label1 = Tex(r"smooth (default)").next_to(line1, RIGHT, buff=0.5)
        label2 = Tex(r"linear").next_to(line2, RIGHT, buff=0.5)
        label3 = Tex(r"there\_and\_back").next_to(line3, RIGHT, buff=0.5)
        label4 = Tex(r"rush\_into").next_to(line4, RIGHT, buff=0.5)

        labels = VGroup(label1, label2, label3, label4)

        self.play(Write(lines), FadeIn(dots), FadeIn(labels))

        # usage in animate syntax (animating moving dots)
        self.play(
            dot1.animate(rate_func=smooth).shift(RIGHT * 4),
            dot2.animate(rate_func=linear).shift(RIGHT * 4),
            dot3.animate(rate_func=there_and_back).shift(RIGHT * 4),
            dot4.animate(rate_func=rush_into).shift(RIGHT * 4),
            run_time=3,
        )

        self.play(FadeOut(lines), FadeOut(dots))

        # usage in normal animations (writing lines)
        self.play(
            Write(line1, rate_func=smooth),
            Write(line2, rate_func=linear),
            Write(line3, rate_func=there_and_back),
            Write(line4, rate_func=rush_into),
            run_time=3,
        )

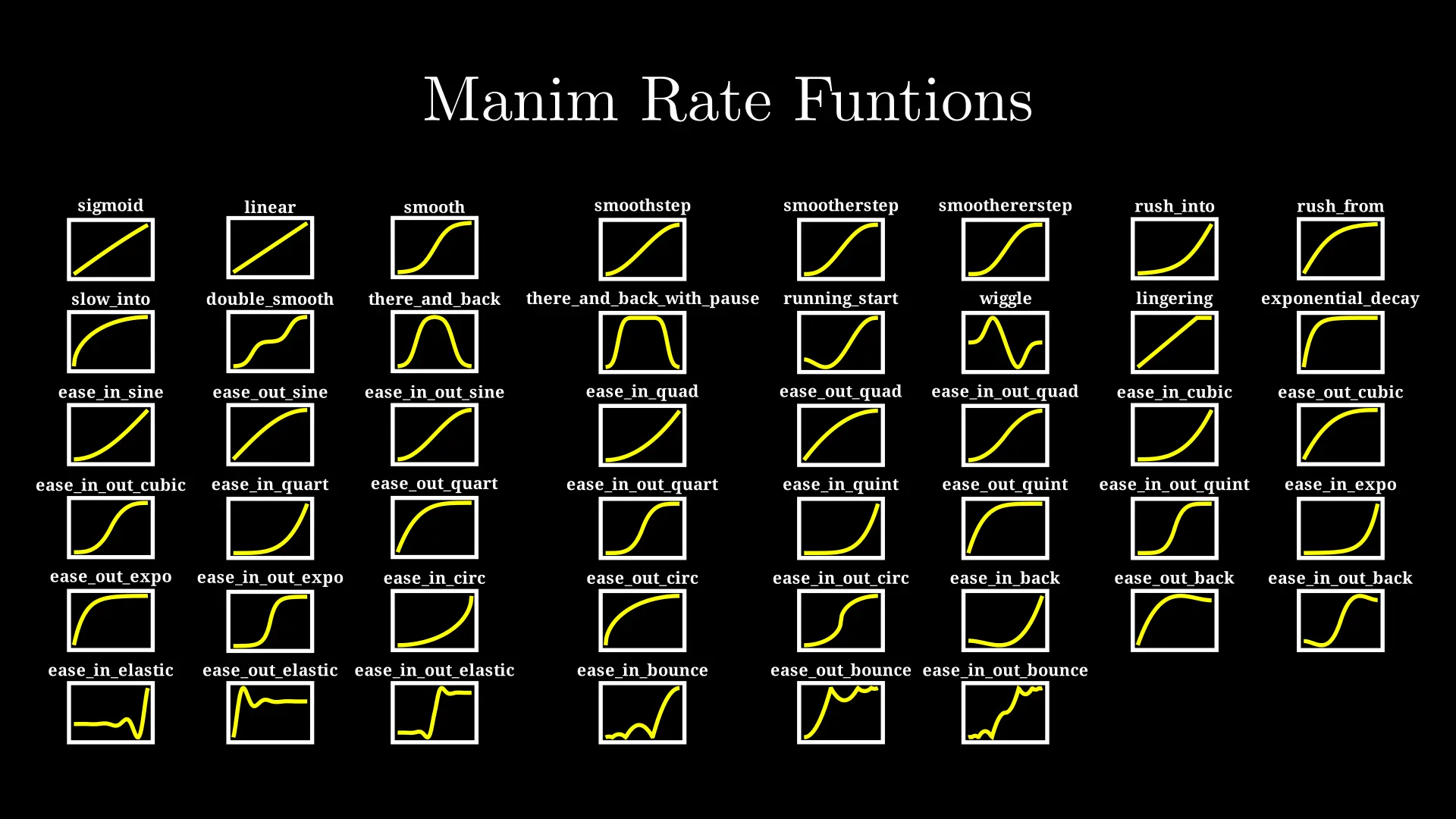
Below is the (almost) complete list of curves that are frequently used in animations. There also exists a wonderful website which contains a number of these functions, including an interactive visualisation of their progress, if you want to experiment with them outside of Manim.

A list of Manim easing curves

Tasks

Graph algorithm

Create an animation of DFS (or some other neat graph algorithm).

Note that the solution to this task might suffer from a bug in Manim’s graph class implementation in the ordering of vertices and edges in AnimationGroup (at least from what I can gather, I haven’t been able to debug what exactly the issue is), which can be solved by manually setting a higher z_index for the graph’s vertices.

1
2
3
# quickfix for a bug in AnimationGroup's handling of z_index
for v in graph.vertices:
    graph.vertices[v].set_z_index(1)

Author’s Solution

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
from manim import *
from random import *
import networkx as nx


class GraphAlgorithm(Scene):
    def construct(self):
        seed(0xDEADBEEF)

        n = 14
        p = 3 / n

        VISITED_COLOR = GREEN
        NEIGHBOUR_COLOR = BLUE

        graph = None
        while graph is None or not nx.is_connected(graph):
            graph = nx.generators.random_graphs.gnp_random_graph(n, p)

        g = (
            Graph(graph.nodes, graph.edges, layout_config={"seed": 0})
            .scale(2.7)
            .rotate(PI / 12)
        )

        # quickfix for a bug in AnimationGroup's handling of z_index
        for v in g.vertices:
            g.vertices[v].set_z_index(1)

        explored = set()

        def dfs(v, position_object):
            """Recursive DFS which moves the position_object."""
            neighbours = list(graph.neighbors(v))

            for w in neighbours:
                if w in explored:
                    continue

                edge = (v, w) if (v, w) in g.edges else (w, v)

                unexplored_neighbours = [w for w in neighbours if w not in explored]
                unexplored_neighbour_edges = [
                    (a, b)
                    for a, b in g.edges
                    if (a == v and b in unexplored_neighbours)
                    or (b == v and a in unexplored_neighbours)
                ]

                # while there exist unexplored neighbours, explore
                if len(unexplored_neighbours) != 0:
                    self.play(
                        *[
                            g.vertices[q].animate.set_color(NEIGHBOUR_COLOR)
                            for q in unexplored_neighbours
                        ],
                        *[
                            g.edges[e].animate.set_color(NEIGHBOUR_COLOR)
                            for e in unexplored_neighbour_edges
                        ],
                    )

                explored.add(w)

                # animation of transitioning to neighbouring vertex
                # has two parts - first initialize the move and then change color (+ flash)
                self.play(
                    AnimationGroup(
                        position_object.animate.move_to(g.vertices[w]),
                        AnimationGroup(
                            Flash(g.vertices[w], color=VISITED_COLOR, flash_radius=0.3),
                            g.edges[edge].animate.set_color(VISITED_COLOR),
                            g.vertices[w].animate.set_color(VISITED_COLOR),
                            *[
                                g.vertices[q].animate.set_color(WHITE)
                                for q in unexplored_neighbours
                                if q != w
                            ],
                            *[
                                g.edges[(a, b)].animate.set_color(WHITE)
                                for (a, b) in unexplored_neighbour_edges
                                if (a, b) != edge
                            ],
                        ),
                        lag_ratio=0.45,
                    )
                )

                dfs(w, position_object)
                self.play(position_object.animate.move_to(g.vertices[v]))

        self.play(Write(g))

        start_vertex = 0

        position_object = (
            Circle(fill_color=VISITED_COLOR, fill_opacity=1, stroke_color=VISITED_COLOR)
            .move_to(g.vertices[start_vertex])
            .scale(0.15)
        )

        self.play(
            Flash(g.vertices[start_vertex], color=VISITED_COLOR, flash_radius=0.3),
            g.vertices[start_vertex].animate.set_color(VISITED_COLOR),
        )

        self.add(position_object)

        # run DFS
        explored.add(start_vertex)
        dfs(start_vertex, position_object)

        self.remove(position_object)
        self.play(Unwrite(g))

Fibonacci sequence

Create animation of the Fibonacci sequence (or some other similar sequence like Pell’s numbers or Lucas’ numbers).

Updaters from the previous part will be very handy. Additionally, the TracedPath class can be used to create the path traced by the dot traveling around the spiral. The animation of the dot travel can be implemented via the Rotate animation, which can be used to rotate one object around another.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from manim import *


class TracePathExample(Scene):
    def construct(self):
        dot = Dot().shift(LEFT)

        self.play(Write(dot))

        # TracedPath accepts a function that returns the position of the object to trace
        path = TracedPath(dot.get_center)

        # we mustn't forget to add the path to the scene for it to get updated!
        self.add(path)

        self.play(Rotate(dot, about_point=ORIGIN))

        self.play(dot.animate.shift(UP))
        self.play(dot.animate.shift(LEFT * 2))
        self.play(dot.animate.shift(DOWN))

        path.clear_updaters()

        self.play(dot.animate.shift(RIGHT * 2))

There is, however, a slight catch: using TracedPath runs into a well-known Manim bug with caching – that’s why we need to use the --disable_caching flag which fixes this bug by not caching the animations.

Author’s Solution

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
from manim import *
from random import *


class FibonacciSequence(MovingCameraScene):
    def create_square(self, size):
        """Create a square of the given size."""
        return VGroup(Square(side_length=size), Tex(f"${size}^2$").scale(size))

    def get_camera_centering_animation(self, squares):
        """Center (and scale) the camera at the given square."""
        h = squares.height * 1.5
        return self.camera.frame.animate.set_height(h).move_to(squares)

    def construct(self):
        squares = VGroup(self.create_square(1))

        self.play(Write(squares[0]), self.get_camera_centering_animation(squares[0]))

        self.camera.frame.save_state()

        n = 7

        # create the squares
        a = 1
        b = 1
        directions = [RIGHT, UP, LEFT, DOWN]
        for i in range(n):
            b = b + a
            a = b - a

            direction = directions[i % 4]

            new_square = self.create_square(a).next_to(squares, direction, buff=0)
            squares.add(new_square)

            self.play(
                FadeIn(new_square, shift=direction * a / 3),
                self.get_camera_centering_animation(squares),
            )

        dot = Dot().move_to(squares[0].get_corner(LEFT + UP)).scale(0.5)

        path = TracedPath(dot.get_center)

        self.wait(1)

        # start the spiral
        self.play(
            squares.animate.set_color(DARK_GRAY),
            AnimationGroup(
                self.camera.frame.animate.restore().move_to(dot),
                Write(dot),
                lag_ratio=0.5,
            ),
        )

        # keep a copy of the dot at the origin
        center_dot = dot.copy()
        self.add(center_dot)

        # for scaling the dot
        starting_frame_height = self.camera.frame.height

        def update_camera_position(camera):
            """Updater k pozicování kamery nad tečkou."""
            camera.move_to(dot.get_center())

        def update_spiral(path):
            """Scale the thickness of the stroke with the zoom of the camera."""
            path.set_stroke_width(self.camera.frame.height / 1.5)

        def update_dot(dot):
            """Scale the size of the dot with the zoom of the camera."""
            dot.set_height(
                center_dot.height * (self.camera.frame.height / starting_frame_height)
            )

        # don't forget to add the path to the scene so it gets animated
        self.add(path)

        path.add_updater(update_spiral)

        self.camera.frame.add_updater(update_camera_position)

        dot.add_updater(update_dot)

        a = 0
        b = 1
        for i in range(n + 1):
            # the directions are defined in a way where neighbouring directions correspond
            # to points around which we want to rotate
            direction = directions[i % 4] + directions[(i + 1) % 4]
            b = b + a
            a = b - a

            # we're zooming by about the golden ratio each rotation (a little less for
            # the animation to look smoother)
            phi = (1 + 5 ** (1 / 2)) / 2
            zoom_coefficient = phi * 0.9

            self.play(
                Rotate(
                    dot,
                    about_point=squares[i].get_corner(direction),
                    angle=PI / 2,
                ),
                self.camera.frame.animate.scale(zoom_coefficient),
                rate_func=linear,
            )

        # cleanup
        self.camera.frame.clear_updaters()
        path.clear_updaters()
        dot.clear_updaters()

        self.play(self.get_camera_centering_animation(squares))

        self.wait(1)

        self.play(
            FadeOut(squares),
            FadeOut(dot),
            AnimationGroup(
                Unwrite(path, run_time=2),
                AnimationGroup(Flash(center_dot, color=WHITE), FadeOut(center_dot)),
                lag_ratio=0.9,
            ),
        )

Langton’s ant

Create an animation of Langton’s ant (or one of it’s color variants).

In each step, the ant moves in the following manner:

if it’s on a black space, turns right; else turns left
inverts the color of the space it’s standing on
moves forward

To create the ant object, you can use the SVGMobject class to render an SVG image (this one, for example, which the author’s solution uses).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
from manim import *


class SVGExample(Scene):
    def construct(self):
        image = SVGMobject("ant.svg")

        self.play(Write(image))

        self.play(image.animate.set_color(RED).scale(1.75))

        self.play(Rotate(image, TAU))  # tau = 2 pi

        self.play(FadeOut(image))

There is one trap in this task, which is using updaters on the ant to track it while moving. This won’t move due to how a center of an object is calculated – by default, it is simply the center of the bounding rectangle of the object, which fails for shapes like the ant.

Author’s Solution

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
from manim import *
from random import *


class Ant:
    deltas = [(-1, 0), (0, -1), (1, 0), (0, 1)]

    def __init__(self, position):
        self.position = position
        self.orientation = 0

    def __get_orientation_delta(self):
        """By how much should the ant move in the current orientation."""
        return self.deltas[self.orientation]

    def __rotate_by_delta(self, delta):
        """Turn the ant in a multiple of 90 degrees."""
        self.orientation = (self.orientation + delta) % len(self.deltas)

    def rotate_left(self):
        """Turn the ant left."""
        self.__rotate_by_delta(-1)

    def rotate_right(self):
        """Turn the ant right."""
        self.__rotate_by_delta(1)

    def move_forward(self):
        """Move the ant forward."""
        dx, dy = self.__get_orientation_delta()
        self.position[0] += dx
        self.position[1] += dy

    def update(self, states):
        """Move and turn the ant, updating its state."""
        x, y = self.position

        states[y][x] = not states[y][x]

        if states[y][x]:
            self.rotate_right()
        else:
            self.rotate_left()

        self.move_forward()


class LangtonAnt(MovingCameraScene):
    def construct(self):
        n = 15
        state = [[False for _ in range(n)] for _ in range(n)]
        squares = [[Square() for _ in range(n)] for _ in range(n)]
        squares_vgroup = VGroup(*[*sum(squares, [])]).arrange_in_grid(columns=n, buff=0)

        ant = Ant([n // 2, n // 2])
        ant_object = (
            SVGMobject("ant.svg")
            .set_height(squares_vgroup[0].height * 0.7)
            .rotate(PI / 2)
        )

        self.play(FadeIn(squares_vgroup), Write(ant_object))

        self.wait(1)

        step_count = 100

        slow_start_iterations = 5
        slow_end_iterations = 3

        slow_run_time = 1
        fast_run_time = 0.07

        for i in range(step_count):
            x, y = ant.position

            new_color = state[y][x]
            rect = squares[y][x]

            running_time = (
                fast_run_time
                if slow_start_iterations < i < step_count - slow_end_iterations
                else slow_run_time
            )

            self.play(
                Rotate(ant_object, PI / 2 * (1 if new_color else -1)),
                run_time=running_time,
            )

            ant.update(state)
            nx, ny = ant.position

            self.play(
                rect.animate.set_fill(BLACK if new_color else WHITE, 1),
                ant_object.animate.move_to(squares[ny][nx]),
                self.camera.frame.animate.move_to(squares[ny][nx]),
                run_time=running_time,
            )

        self.wait(1)

        # determine the currently filled squares to move to them
        white_squares = VGroup()
        for i in range(n):
            for j in range(n):
                if state[i][j]:
                    white_squares.add(squares[i][j])

        self.play(
            self.camera.frame.animate.move_to(white_squares).set_height(
                white_squares.height * 1.2
            )
        )

        self.play(FadeOut(squares_vgroup), FadeOut(ant_object))