 Generative Neural Networks
Generative Neural Networks
Note: these notes are in a pretty questionable state (at least after the first few lectures) – there are lot of TODOs that I won’t do. If you’re taking this class and have better notes, I’d be happy to update the website.
Preface
This website contains my lecture notes from a lecture by Ullrich Köthe from the academic year 2023/2024 (University of Heidelberg). If you find something incorrect/unclear, or would like to contribute, feel free to submit a pull request (or let me know via email).
Introduction to generative modeling
- assumption:
- “nature” works according to some hidden mechanisms (complicated probability distribution)
- is sampled from the true probability / generating process (or )
- we have a training set
- use to learn
- goal:
- find approximation (for )
- two aspects of generative modeling (neural network can usually do both):
- inference – given some data instance , calculate value of
- generation – create synthetic data which is indistinguishable from real data
- downstream benefits of generative modelling
- powerful tool for humans (e.g. chat bot as personal teacher)
- great for things that are well-established
- poor for things that aren’t (tends to hallucinate)
- helps to produce insight: identify important factors influencing the outcome
- ex. “symbolic regression”: find / learn analytic formulas to explain the reality (vanilla neural networks are black boxes)
- use for decision making: is treatment better than treatment for patient ?
- powerful tool for humans (e.g. chat bot as personal teacher)
What I cannot create, I do not understand. (Richard Feynman)
Warm up: 1D generative models
Basic principle: is complicated reduce it to something simple.
- introduce new variable (“code”) for deterministic function s.t. the distribution is simple
- we’ll be actually doing it he other way – pick and learn (will be a NN)
- for generative modeling to work, we additionally require that is invertible
- if – inference direction
- if – generative direction
- called “inverse transform sampling'
- consequence in 1-D is that must be a monotonic function (increasing by convention)
- (strictly monotonic requires )
- universal property of monotonic functions (saw proof in the lecture):
Apply to probability distribution:
- define mass in interval as
- for the Gaussian distribution, gives about ( gives )
- is permissible, if for every interval :
Now we can substitute , getting
which must hold for any interval , meaning
which is called the change-of-variables formula, allowing us to express the complex distribution in terms of the simple distribution, transformation and its derivative (this is where the fact that it’s always positive comes in handy, since it’s just a scaling factor).
For 1D, works well (numerically easy, a generator is available anywhere)
- e.g. Mersenne twister (based on Mersenne primes)
- for that, we get and so the CDF is
- if then (integral over nothing)
- if then (integral over everything)
- if then because
Ex.: exponential distribution
for hyperparameter normalization, which has to be
To get , we again do the integral with upper bound being , getting
To sample from it, we solve for in the equation above and get
which is either inverse CDF, quanti function or the percent-point function (PPF)
There was another example of a Gaussian PDF/CDF/PPF. Unlike the exponential, it the CDF doesn’t have a closed-form solution and has to be approximated.
Ex.: and need not be continuous (they can have jumps) – Bernoulli
We want to make it continuous, we do embedding via the -distribution
- the delta funtion is very handy: for any function ,
- are atoms – their probability is not zero (unlike functions like Gaussian)
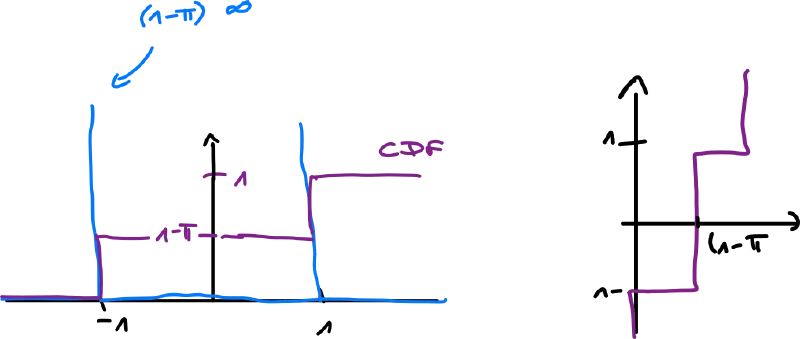
Ex.: spike-and-slab distribution
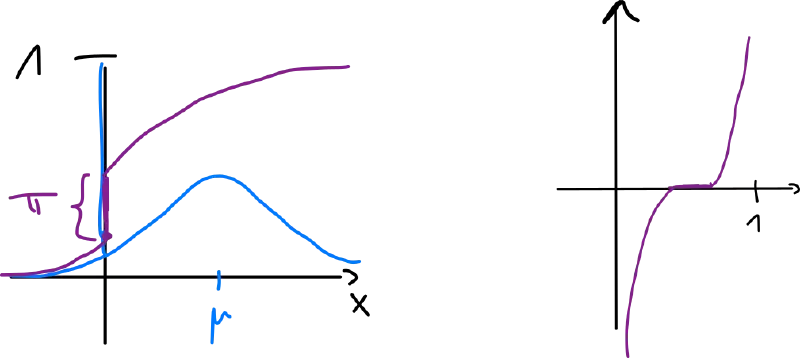
Classical approaches
What if we don’t know but we have a ?
- histogram – define (smallest value), (bin width)
- the “inter-quantile range” is obtained by sorting TS and getting the difference between values and (i.e. quarter to the left, quarter to the right)
- the formula gives a good balance between number of bins vs. the number of items per bin
- generalization of a histogram – mixture distribution
- idea: express a complicated as a superposition of simple , i.e.
- is weight, is some simple distribution
- (has to be a probability distribution…)
- for histogram, is uniform
- for Gaussians, we have Gaussian mixture model (GMM); solved with the EM algorithm
- idea: express a complicated as a superposition of simple , i.e.
- kernel density estimation (or any other simple distribution)
- (one component per training sample)
- similar to mixture distribution (has less distributions), here is the hyperparameter
Warmed up: more dimensions!
Extensions of classical approaches
multi-variate standard normal
- can be expressed as a product of 1-D normal distributions:
- sampling in dimensions boils down to many samplings in 1-D
multi-variate Gaussian distribution with mean , covariance
- to sample, we compute the eigen decomposition of (for orthonormal and diagonal with eigen values) and do the following:
- invert (inverse is transposition for orthogonal)
- then
- define new coordinates
- then
- we can sample 1-D gaussians and put them in the vector, which we invert
- : reparametrization trick (from arbitraty Gaussian to std. normal)
- in our language:
- to sample, we compute the eigen decomposition of (for orthonormal and diagonal with eigen values) and do the following:
- similar for other analytic multi-variate distributions (
scipy.statsoffers ~16)
What if must be learned?
Mixture model idea naturally generalizes to dimensions:
- histograms are defined by a regular grid with levels per dimension (exponential, does not scale)
- solution: define bins by recursive subdivision (eg. density tree)
- quality of the models is only medium – each subdivision doubles the number but looks at only one variable, which is bad if you have 100s of variables… the number of coorelations to be considered is bounded by tree depth, which must be
- for Gaussians, we have to learn co-variance (instead of variance) change the EM algorithm accordingly
- kernel density estimation is also unchanged, but finding a bandwidth that works equally well is very difficult
- (2.) and (3.) become more expensive for growing
- sampling is simple: sample , sample
Reducing to many 1-D distributions
- naive: , learn a 1-D model for each coordinate
- assumes variable indepence, we loose all coorelation (highly unrealistic)

- exact: auto-regressive model – decompose by Bayesian chain rule:
- any ordering of the chain rule also works (variable order is interchangeable)
- each is a collection of 1-D distributions (one distribution per value of )
- use conditional inverse transform method
- then which is auto-regressive (values rely on the previous ones)
- problem: is a different 1-D function for each value of
- eg. if is defined on a regular grid with levels per dimension, then we have different values does not scale
- general solution: learn with a neural networks
- generalizes from a few seen (TS) values of to all possible values
- simpler solution: if (independent) then can be dropped
- also, if for then can be dropped
- repeat with more complicated conditions, dropping as many as possible
- example: Markov chain: – the DAG becomes a chain
- typical if is a timestep (future only depends on the present, not the past)
- easy to learn
- example: causal model for causal parents of
- e.g. both earthquake and burglar cause the alarm (not the other way lmao)
- causal DAG has the fewest edges (i.e. easier to learn) BUT finding it is very hard
Measuring model quality
- we can measure “distance” between and (even if we don’t know ) to:
- use as objective function for training
- use for validation after training
Forward KL divergence
A few useful properties:
It’s a divergence and not a distance (i.e. a metric) – not symmetric, triangular inequality doesn’t hold
There was an example here with a discrete distribution.
Caveat: if there are datapoints in s.t. but , then
- can’t be used as training gradient (since it’s infinity)
- use model families s.t.
Relationship between forward KL and maximum likelihood training:
- entropy is independent of and can be dropped, so get an optimization problem
- minimize KL minimize NLL maximize for
Given ,
- does not contain we can optimize without knowing (samples sufficient)
- but we need to calculate during training must be capable to do “inference”
Reverse KL divergence
- empirical approximation: iterate :
- current guess : draw batch
- need to know … cannot be used in many application
- useful when we know the distribution but it’s intractable (ex. Gibbs distribution)
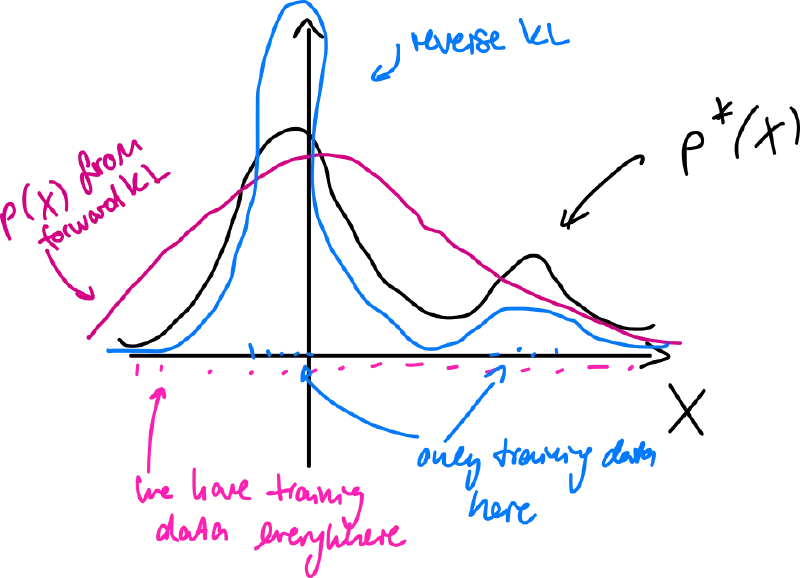
Comparison (forward x reverse)
- forward KL tends to smooth out models of – mode-covering
- reverse KL tends to focus on single (or few) highest modes – mode-seeking/collapse
Maximum Mean Discrepancy
The idea is to use the kernel trick
- without kernel:
- define
- two data sets
- calculate
- (if when )
- is a metric
- : witness function – certifies that and are different when is big
- family function must be chosen s.t. we can’t cheat (i.e. arbitratily add/multiply to increase – e.g. conditions on variance)
- now replace explicit mapping with a kernel function :
Typical kernels (for hyperparameters):
- squared exponential
- inverse multi-quadratic
- multi-scale squared exponential
Generative Modeling with NN
- relationship between generative modeling and compression: both are essentially
- lossless: (e.g. ZIP)
- idea: use short codes for frequent symbols and longer for more rare symbols
- lossy compression: (e.g. JPEG)
- idea: decompose into smaller parts, drop important stuff, use lossless compression for important stuff
- lossless: (e.g. ZIP)
Here we have 3 conflicting goals:
- small codes:
- accurate reconstruction: (for some distance function)
- preserve data distribution: (for some distribution)
Note that (shown during lecture).
Autoencoder
learned compression: and are neural networks
- lossy compression because usually
- “bottleneck” is a hyperparameter
- train by reconstruction error
- lossy compression because usually
distance functions for the loss:
- is most common
- tends to be less blurry for images (better preserves small details)
- multi-resolution : compute image pyramid (apply loss to different image sizes)
denoising autoencoder: add more noise to the data to teach the network what noise is
- better, deep mathematical properties later
autoencoder is not a generative model (according to our definition):
- we haven’t learned the distribution – no generative capability
- no inference, i.e. no way to calculate
Generating data
expert learning of by a second generative model
- often simpler than learning directly (e.g. )
- Stable Diffusion (image generation) does this
joined optimization:
- predefine (desired code dimension)
- measure add new loss term
- choosing a kernel is another hyperparameter
- paper: variant of INfoVAE [2019]
variational autoencoder (VAE) [2014]
- idea: replace deterministic functions and with conditional distributions
- encoder: , decoder
- we also have data and desired code dist.
- implies two version of joint distribution of and
- encoder (Bayes)
- decoder (also Bayes)
- two requirements:
- decoder marginal
- encoder-decoder pair must be self-consistent:
- here we will use the loss:
- trade-off between two objectives:
- reconstruction error minimized if encoder & decoder are deterministic with perfect reconstruction
- first term minimized if – encoder ignores the data, which is the opposite of perfect reconstruction
- trade-off between two objectives:
- maximizing loss enforces (2) (proved during the lecture)
- in literature, is usually maximized
- conceptually, minimizing is simpler
- maximizing the also indirectly maximizes the data likelihood under the model – ML principle: TS should be a typical model outcome
- minimize expected negative log-likelihood (NLL) (proved during the lecture)
- is an upper bound for NLL loss
- most common implementation encoder and decoder are diagonal Gaussians:
- since we only have diagonal Gaussians, we can’t rotate the ellipses
- since we only have Gaussians, the shape is restricted to circles
- if then can be calculated analytically
- if , reconstruction error becomes squared loss
- downscales squared loss reconstruction error unimportant
- upscales squared loss reconstruction error dominant
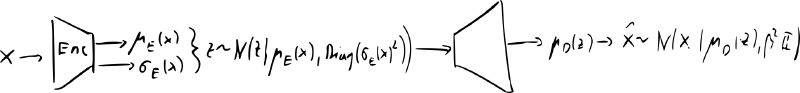
- generation:
- inference: if and then must give the same value for all
- idea: replace deterministic functions and with conditional distributions
conditional VAE
- instead of learning , we learn for some variable
- e.g. for MNIST label
- if encoder & decoder are Gaussians, add as input to the networks
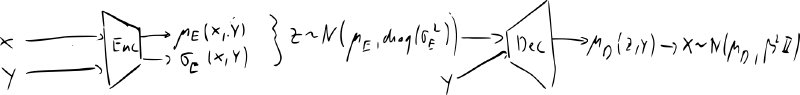
- we can supply different labels for encoding / decoding – style transfer
- one digit in style of another / one image in the style of another
- here we can do operative classification: test with unknown label, try encoding with every label and calculate the corresponding , returning the one with maximum probability
Generative Adversarial Networks (GANs)
- dominant generative model 2014-2019/20
- now diffusion models and transformers are better
- idea: learn quality function (instead of hand-crafted formula like MMD)
- new NN “discriminator/critic” – classifier vs.
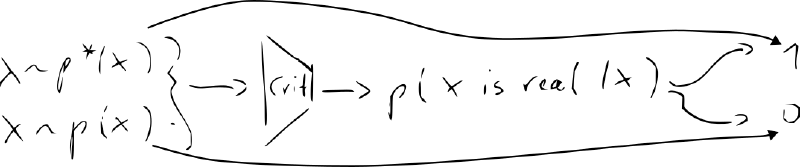
- train the decoder (“generator”) jointly with the critic
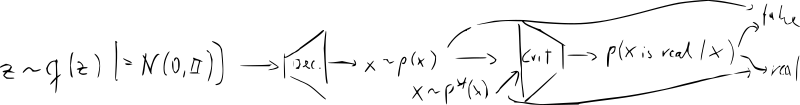
- new NN “discriminator/critic” – classifier vs.
- training becomes a game:
- critic becomes better at distinguishing reals and fakes
- decoder becomes better at fooling the critic
- training objective
- at optimal convergence, we have (~proven during the lecture)
- assumes that we have a perfect critic and proves from there
- in practice, we don’t have a perfect critic (and it wouldn’t work in practice because for the bad decoder, recognizing fakes is easy so gradient will be zero and we won’t train anything)
- instead, train and jointly (both random initially) via alternating optimization – one step for , one/more steps for
- also use non-saturating loss – replace with
- global optimum is preserved, should work better for training
- see the graphs for vs.
- GANs defined state-of-the-art up to 2019/20:
- WassersteinGAN: uses alternative loss for critic (not really better)
- CycleGAN: replace with true distribution over another variant of real data
- e.g. dist. of daylight photos, dist. of night photos
- two cases:
- paired dataset (same from both variants) – supervised learning
- unpaired dataset (no overlap between instances)
- we have new “cycle losses” – and should be small
- for paired, we additionally have and
- we still need a critic, otherwise and are identity (must combine with cycle loss)
- as opposed to GAN, we have no bottleneck – and are the ~same dimensions
- InvertibleGAN: add an encoder to original GAN
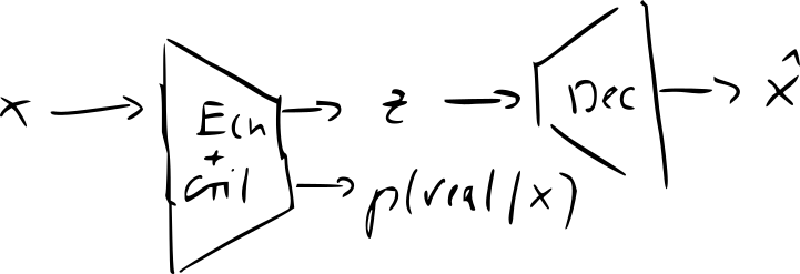
- recreating codes and distinguishing reals from fakes can use the same image features same network to encode and decode
- many more additional losses (similar to CycleGAN)
- hyperparameter optimization is hard
Normalized Flows (NF)
- one of the major recent approaches
| Goals | Autoencoder | VAE | GAN | NF |
|---|---|---|---|---|
| small codes | hyperp. | hyperp. | hyperp. | lossless |
| accurate distribution | bad (doesn’t care) | trade-off | good | good |
| good reconstruction | good | trade-off | can’t | good |
Idea: generalize the inverse transformation method to arbitrary dimensions:
- high-dimensional density, a region
- define
- let an invertible encoding,
- the image of in -space:
- we want consistency: for all
- apply the multi-dimensional change-of-variables formula: for the Jacobian (matrix of partial derivatives) of
Since consistency must hold for any , the integrals must be equal, we get the multi-variate change-of-variables formula
Goal:
- pre-define , e.g.
- learn s.t. ( neural network)
Recall the -D case:
- for learning is better:
- has non-zero gradients for gradient descent
- supported on all of (unlike uniform – what to do with points outside?)
Two difficult problems in practice, covered in the next sections:
- how to ensure that is invertible & efficiently compute
- how to (efficiently) calculate
(2) Calculating
- 2-D case is easy:
- for higher cases, we can calculate determinants recursively, which grows exponentially
- general solution with SVD:
- effort of , which is a little better than exponential
- we can also expoit special case if is triangular (and the diagonal is non-zero, otherwise the determinant is zero), in which case is just the product of the diagonal elements
- we already talked about an instance of this: auto-regressive models – since they rely on the previous terms, the Jacobian is triangular and the determinant is very easy
If is a multi-layer network, is a composition of functions
- the Jacobian of comosition is the product of all Jacobians (consequence of chain)
- the determinant is the product of determinants (consequence of linear algebra)
- determinant of multi-layer network is easy when layer determinants are
- popular architecture is to define all as auto-regressive functions
(1) Ensuring that is invertible and computable
- trick: chose auto-regressive and easy to invert
- major architecture: Coupling layer network is “real NVP” (non-volume-preserving due to the determinants being non-unit)
- auto-regressive model
- in each layer, change only half of the dimensions of
- pass the remaining dimensions on unchanged (“skip connection”)
- no surprise since it’s a variant of the auto-regressive model
- simplest invertible function – affine functions:
- and are neural networks that we train: (same for )
TODO: add the drawing here
- for to be invertible, we need
- we actually learn and set
- also takes care of the sign of the Jacobian – no abs!
- in practice, it is numerically more stable to set
- we actually learn and set
Summary
forward:
inverse:
invertible layer constructed from non-invertible and
choose and according to architecture (fully-connected, convolutional, etc.)
determinant of an affine coupling layer
RealNVP
- invertible NN with autoregressive form, i.e. is easy
- after each coupling layer apply orthonormal transformation , e.g. permutation
- have and so easy to work with
- it turned out experimentally that learning is not necessary, no one knows why
- fixed matrices are sufficient / may change with new learning algorithm
- final architecture:
- training algorithm: minimize negative likelihod of data (derivation in slides):
- the slides here explain why affine coupling works
Spline coupling
- better than affine coupling for low dimensions ()
- uses Hermite splines, which require location of knots, function at knots and derivatives at knots (with interpolation in between)
- most popular: rational quadratic spline [Neural Spline Flows, 2019]
Conditional derivatives
- e.g. is digit label, is MNIST
- : sample any digit
- : sample only s
- typical setup for supervised learning:
- traditional networks point estimates (regression or classification)
- conditional NFs: distribution of estimate uncertainty of
- an autoregressive function is easy to generalize for conditionality:
- can be added as an input to all nested networks
- works if is known for both forward and backward network execution
- if is complicated (e.g. high dimensional image), we have shared preprocessing network (feature detector / summary network), which can
- use architecture of an existing regression networks minus the last layer
- use a foundational model trained by the big guys on big data
Simulation-based inference (SBI)
setting:
- is observables, i.e. variables we can measure
- are hidden properties, i.e. variables we’d like to know but can’t measure
assumptions:
- hidden variables are more fundamental, e.g. is caused by
- we have a scientific theory how the arrise from the (forward process)
- theory is implemented as an algorithm computer simulation
- we can do “in-silico experiments” (as opposed to “in-vivo” and “in-vitro”)
- three types of variables:
- : inputs to the simulation (pretend we know the hidden state)
- : outputs
- optionally : random variables for non-deterministic simulation
- deterministic (the simulation program)
- non-deterministic – “noise outsourcing”
simulation paradigm: if we knew , we could predit
- since we don’t know , try multiple and generate alternate scenarios
- during covid, get various assumptions about the virus and about prevention measures () and simulate what happens (), getting various scenarios
- it’s hard to select a good set of s – SBI improves upon this
- since we don’t know , try multiple and generate alternate scenarios
two important special cases of the structure of :
- mixed effects model
- for , sample and
- look at the group first, then differentiate for each individual
- , but (independent conditionally based on the global assumptions)
- dynamical systems (time-dependent behavior)
- for ,
- look at the group first, then differentiate for each individual
- if is continuous, we get a stochastic differential equation
- if is discrete, we get a hidden Markov model
- , but (if Markov property is fulfilled) \end{cases}]
- mixed effects model
Main tasks of SBI
- surrogate modelling: train a model that emulates the simulation
- good for speed-up (since is often slow)
- forward inference: often, only defines implicitly, but doesn’t allow to calculate (“likelihood-free inference, implicit likelihood”)
- approximate true likelihood by
- inverse inference: run the simulation backwards:
- usually intractable (no analytic solution) and/or ill-posed (no inverse)
- traditional solution would be to pick constrainst & regularization that select one
- SBI solution: pick probabilistic via Bayes rule
- define equivalence classes
- all s that could have produced given
- posterior assigns a “possibility” to every
- problems:
- if likelihood is only implicitly defined then Bayes rule canot be calculated (i.e. surrogate model above)
- even if (or a surrogate) is known, Bayes rules is usually intractable
- learn generative model for posterior
- define equivalence classes
- model missclasification & outliner detection – a simulation is not reality:
- use SBI to detect if
- this and observed outcome compatible with
- if not, the simulation is unrealistic – “simulation gap”
- is a set of outcomes compatible with ?
- model comparison and selection
- if we have competing theories
- determine which describes best (if any)
- digital twins: in a mixed effects setting, given
- determine and accurately enough to predict
- the same treatment that worked on this pacient will work on this one too
- classical: base treatment decisions mainly on (“treatment guidelines”) after an appropriate stratification of population into subgroups
- desired: “precision medicine” – use and
- determine and accurately enough to predict
- experimental design and active learning: how should we measure to learn as much as possible about with given experiment budget?
Classical approaches for inverse inference
- conjugate priors – chose and such that can be analytically calculated and is in the same distribution family as ( incremental Bayesian updating)
- common is the Gaussian (surprise surprise) but exists for many other distributions
- efficient and mathematically elegant
- very unrealistic big simulation gap (usually picked for convenience)
- likelihood-based inference – and are known (not just )
- but is intractable (so we can’t use Bayes rule)
- create a sample using Markov chain Monte Carlo (MCMC)
- important relaxation: can be unnormalized (e.g. Gibbs distribution)
- very general, has lots of mathematical theory
- implemented in many libraries/languages
- not amortized – runs from scratch for each new
- expensive – must be very large for complete “mixing”, i.e. until all modes of have been covered
- often, a long “burn-in” phase is needed to forget a bad initial guess
- throw away
- samples and are close to each other (chain moves slightly away from the previous guess) – may bias derived statistics of the chain (i.e. both are rejected)
- skip each th samples in the chain
- often difficult to define proposal distribution that has low rejection rate
- only applicable when is not large and not too slow
Algorithm (MCMC):
- given, arbitrary initial guess
- pick a “proposal transition distribution” for transition prob
- is a hyperparameter, e.g. a Gaussian – something easy to work with
- pick a “proposal transition distribution” for transition prob
- for
- sample a proposal
- calculate acceptance weight
- sample – acceptance threshold
- if : accept (), else reject ()
- theory: for ,
- likelihood-free inference – is unknown and only implicitly defined as
- only samples with
- Approximate Bayesian Computation (ABC) brute force
- requires a distance for outcomes, usually hand-crafted
- works when MCMC doesn’t
- implemented in many libraries/languages
- very slow – if is small, the model is more precise and slower
- not amortized
- hard to define if is complicated or is high
- design hand-crafted summary statistics and compare
- only applicable when is not large
Algorithm (ABC):
- , sample (we later become
- repeat until
- sample , simulate
- if , add to samples and increase , else reject
- if we were lucky with , we accept; otherwise reject
Doing it better with NN
amortized SBI – given
- noise often independent of (i.e. just a random number)
- easy to create when we know and
- we can train conditional normalized flows for
- (forward surrogate)
- (inverse posterior)
- likelihood-free – not needed, suffices
- scales to high dimensions for both and
- can learn summary statistics s.t.
- amortized – all simulations in the TS contribute to the training, no rejections
- upfront training effort may be high (roughly as expensive as to MCMC runs)
- training amortizes if one analyzes many
- prediction is very cheap (just NN evaluation on the GPU)
- generalization: networks generalize to unseen pairs
- even far from which would normally be rejected contribute to accuracy
- (so far) no theoretical performance guarantees
- (so far) no cheap way to finetune networks when or change slightly
e.g. inverse kinematics – consider 2D robot arm with 4 DOF
- information loss when doing the forward kinematics (4D to 2D)
- the simulation is defined as follows:
- priors (“preferred joint positions”, “convenient situations”)
- independent
- (radians)
- given desired hand location , compute
- for all
- if is inconvenient according to prior
- if is convenient according to prior
- joint probability

Validation of generative models (especially SBI)
- fundamental problem: if , there is no single correct outcome
- traditional testing doesn’t work
- must compare distributions, no individual outcomes
- case: for prior, we have for fixed
- easily generated by simulation
- case: for posterior, we have
- to generate for fixed , we need a classical algorithm (like MCMC or ABC)
- we can compare means/covariances of and – quick check, complete if is Gauss
- can also compare higher order momentums but this tends to be expensive
- plot marginal distributions in 1D and 2D for features
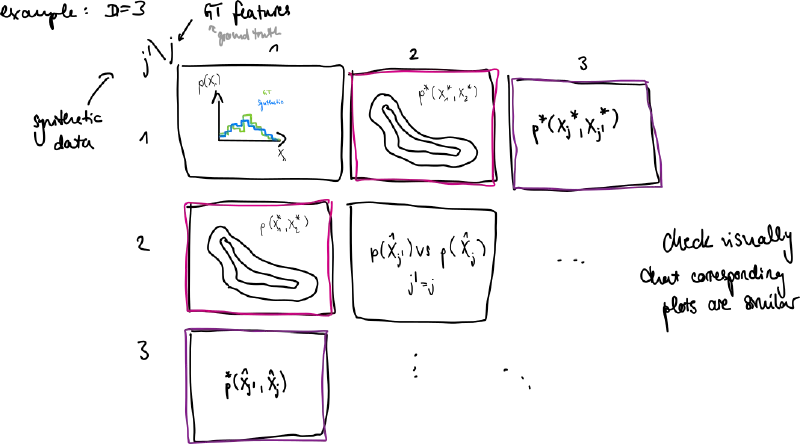
- we don’t see correlations for higher dimensions but errors here can already be apparent
- various scores to compare the samples and (usually ):
- (we already saw) MMD
- Fredechet Inception Distance (FID) – popular if is an image
- idea: compare means and covariance matrices via Fredechet distance
- if they are Gaussian, the Fredechet distance (otherwise complicated) can be computed analytically as
- for images Gaussian assumption is not fulfilled calculate FD in some feature space
- typically, use a pre-trained network (traditionally Inception network, nowadays some foundational model eg. CLIP or DINOv2)
- if no pre-trained model available, we can still use a random(ly initialized) network
- density & coverage (heuristic version of MMD?) [Naeem et al 2020]
- use nearest neighbor method, usually applied in a feature space to make Euclidean distance plausible
- define ball with center and radius for of the -th nearest neighbour of
- is a kernel (the relation to MMD)
- density =
- high when the are close to the
- if all synthetic data is covered
- coverage =
- counts how many of the balls around contain a
- if the synthesized data nicely covers the real data
- case but we also don’t have
- must evaluate on the basis of only, possibly with a single instance
- e.g. grayscale coloring – we only have one GT image that we created the grayscale one from
- check the diversity of the generated sample (always possible without any GT)
- by diversity, we mean that are all different and ideally cover the entire
- Vendi score [Friedman & Dieng 2023]
- calculate kernel (Gram) matrix :
- (can also be done in a feature space)
- (missing in the paper) centralize as in kernel PCA (see MLE)
- calculate eigenvalues of
- calculate eigenvalue entropy (with )
- profit?
- acts as an effective rank of
- if all points are far from each other: for and (max diversity)
- if all points are equal, , we only have one non-zero eigenvalue and
- choosing kernel bandwidth correctly is critical to avoid the extreme cases
- calculate kernel (Gram) matrix :
- must evaluate on the basis of only, possibly with a single instance
Validation of SBI
- given and
- case: compare the distribution of samples via methods from last lecture (MMD, FID, density/coverage)
- case: compare diversity of different approximations via Vendi score
- case: important case in practice
- in SBI, create GT via forward simulation,
- is a GT example for with
- weather forecast:
- rain probability – we can check how well it worked tomorrow
- idea: “calibration” – merge instances with same predicted confidence in a joint test set
- among all days with rain prob. it should have rained in of the cases
- assumes that this is a reasonable thing to do (what if climate change?)
- applied to classification: is and it answers right…
- of the time – well calibrated
- of the time – underconfident
- of the time – overconfident
- realization:
- merge
- sort the merged set as – GT should be uniformly placed
- algorithm:
- given GT , sample
- sort the joined set
- (for index of in sorted order)
- repeat this for many instances
- evaluate (it should be uniform) via histogram – if model is calibrated,
- TODO: graphs of what can happen – skewed - mean is wrong / canyon - overc. / valley – underc.
- caveat: well-calibrated does not imply accurate
- if the model is bad and it knows it, it’s still calibrated
- example: time, sample mean on day
- marginal is
- TODO: finish this, it’s weird
- the lecture has an alternative solution via empirical CDF of s
- we don’t have a hyperparameter (calculated automatically), which is useful
- joint calibration checks: instead of using on one feature at a time, check the entire vector
- reduce the problem to 1-D via “energy” or “surprisal” distribution
- probably TODO here since I got really lost; there should be an algorithm here
- in SBI, create GT via forward simulation,
There is a missing lecture here! See slides for what was in it.
Epidemology: SIR model
- an example of SBI
- [Kermach & McKendrick 1927]
- Susceptible : people who are healthy but can get infected
- Infected : people who are ill and can transmit
- Recovered : people who recovered and are now immune
- simplifying assumptions:
- stationary dynamics: behavior of virus/bacteria and people does not change over time
- no mutations, no countermeasures
- only consider averages over all people in each compartment (, , )
- all people in the same compartment are considered identical
- stationary dynamics: behavior of virus/bacteria and people does not change over time
- traditional non-probabilistic parameter fitting: least squares
- makes the simulation reproduce the real observations as closely as possible
- might get stuck in bad local optima (if the simulation isn’t linear with Gaussian noise)
- disregards uncertainty and ambiguity in
- amortized SBI learns a GNN for
- using a large of synthetic data ()
- design model:
- a healthy individual meets on average people per day
- infected people are not isolated, but meet others as usual
- a fraction of the meetings is potentially contagious
- a fraction of all the dangerous meetings actually leads to transmissions
- if we observe a reduction in infections, we cannot distinguish if people became more cautious ( goes down) or the virus is less infections ( goes down)
- can only recover
- nobody dies and infected people recover after days
- the rates are the following:
- number of new infections per day:
- number of recoveries per day: (for recovery rate)
- write the dynamics as a system of ordinary differential equations – each line is the change in the compartment:
- can divide all equations by , getting normalized values:
- to solve equations, must define :
- given , we can solve the ODEs for any time by “integration”
- Euler forward method: discrete timesteps , approximate
- same for other equations…
- theory says that it’s a good approximation if is small enough
- more sophisticated: Euler backward, Runge-Hutta that allow for larger timesteps
- Euler forward method: discrete timesteps , approximate
- define observables :
- repeat on every day (number of new infections and newly recovered)
- observations are not perfect observation model
- reporting for delay
- underreporting:
- there is some noise going on
- exact values:
- measured values:
- we get relative error, because we’re multiplying
- same for others (noise can be same / different)
- full simulation:
- usually
- should be chosen according to epidemiological prior knowledge
- TODO: equations for the simulation
- get the true values from ODE, calculate noise from the observables (diff between truth and what we can measure)
- we can’t observe the actual state (ODES) but only the noise
- full algorithm:
- define the simulation and priors and
- use the simulation to generate synthetic TS
- setup architecture of GNN
- TODO: image here
- train SNF & summary network jointly using NLL loss:
- will become optimally informative for
- validate (check calibration, sensitivity, etc.)
- tells us that it models the synthetic data well, not the real data
- infer for real data
- check for potential simulation gap ( simulation is unrealistic)
New lecture here, we’re doing SBI for epidemiology again.
a typical person will on average transmit to
healthy people (duration times change of infection times average number of healthy people the person meets in those days)
basic reproduction number is [R_0(t) = \delta \lambda(t) \begin{cases}
1 & \text{new infections go up} \ <1 & \text{new infections go down} \end{cases}] (here is a function of if there are eventually countermeasures / disease mutations)
replacement number [r(t) = R_0(t) [S(t)] \begin{cases}
1 & I(t)\ \text{grows} \ <1 & I(t)\ \text{shrinks} \end{cases}]
two possibilities to end disease:
- herd immunity – when
- by countermeasures – reduce s.t. (regardless of )
if changes over time, learning identification problem becomes much harder
for a simulation to be realistic, implementing the fundamental mechanistic equations is not enough – a realistic model of observation uncertainty is required
- (use squared loss in traditional inverse inference assumes additive Gaussian noise with constant variance)
- model reporting delays
Making things more complex (because we can)
- new things:
- deadly disease – introduce new compartment (dead) with new variable for how many die
- immunity lost after a while – transitions
- vaccination – transition
- imperfect immunity – new compartment (like but with )
- refine infection:
- incubation period (carrier) – infected but cannot transmit
- (with new variable for when they can transmit)
- some (many) infections are undetected
- split into “treated” (knows its infected) and “spreader” (can transmit without knowing it)
- incubation period (carrier) – infected but cannot transmit
- further refinements:
- split into risk groups (e.g. by age, sex, etc.)
- spatial relations (hot spots, travel)
- spatial compartments
- discrete – every node becomes an SIR model, edges are spatial transmissions
- continuous – PDE (partial differential equations)
- spatial compartments
- change over time based on a lot of factors
Checking if the simulation is realistic
- different to calibration – here we have outside data (as opposed to the internal validation where we have our own data)
- Is (real observation or from a competing theory) covered by our SBI model?
- yes can be trusted (if our model is well calibrated etc.)
Idea: if is an outlier of the marginal then networks have not seen data like it during training:
- learn a surrogate for (expensive, big neural network)
- get outlier detection almost for free: we have a summary network
Continuing with new lecture here.
Model misspecification detection: is an outlier?
- if yes, reject and answer “idk” 🤷
- trick: exploit the feature detection network: add loss to pull summary feature distribution towards standard normal
- reject if is an outlier of
Model comparison & selection (between competing theories): measuring training error might not be enough because of overfitting.
- need tradeoff between model accuracy and complexity (“Occam’s razor”)
- classical model selection criterion:
- Akaika criterion (for the size of the model)
- if both models are equally good but one is smaller, it wins
- Bayesian information criterion: (for dataset size)
- Akaika criterion (for the size of the model)
- classical model selection criterion:
Some more stuff was here but brain small.
External validation algorithm:
- given competing theories
- epidemiology: different compartments, priors, observation uncertainty etc.
- create synthetic training data
- train a separate SBI model for each with so that
- perform internal validation for each , redesign until successful
- train a sofmax classifier using combined
- external validation given
- model misspecification detection
- compute logits of model classifier (penultimate layer, before sofmax)
- define classifier
- model comparison by posterior odds
Parameter degeneracy
- sometimes, some elements in cannot be fully identified from
- correlations in the posteriors
- example: epidemiologist write SIR equations in terms of natural/conceptual parameters
- : average number of people a healthy person meets per day
- : fraction of meetings leading to transmission
- in SIR equatoins, we always have cannot distinguish them, but can infer
- if we still use posterior shows the degeneracy (infinitely many pairs () for fixed )
- degeneracy is easy to spot, but generally difficult and hard to distinguish from bad convergence of neural network
Lecture talks about SoftFlow here which addresses this issue for cNFs.
- do not confuse with NoiseNet, which adds the noise to (here we add to )
This lecture had slides with some interesting use cases of the methods that we previously discussed.
Hierarchical models for SBI
- split hidden parameters into
- – global (for the entire population)
- – individual (for every instance)
- example – virology:
- – properties of a patient (& disease)
- – properties of individual cells we analyse
- simulation:
- (standard SBI)
- (for every individual)
- for
- common simplification is
Here we discuss Estimation of a non-linear mixed effects model [Arruda et al 2023].
SINDy-Autoencoders
- “Sparse Identificator of Non-Linear Dynamics”
- we have a dynamic system that produces real-world measurements
- observation takes place in a different coordinate system (e.g. measurements of the planets from earth’s perspective/unknown canonical coordinates)
Two lectures were spent on this.
Physics-informed Neural Networks (PINNs)
- idea: use physical prior knowledge explicitly
- (so far SIB knowledge only used to create training set)
- PINNs: incorporate knowledge into training
- PINNs focus on surrogates for forward problem
- reminder: SBI –
- surrogates learn the likelihood (what we focus on now)
- SBI usually learns posterior of inverse problem ()
- reminder: SBI –
- typically, PINNs only give a single solution, not a distribution
- i.e. learn for and fixed (known or learned)
- PINNs address the case where is a function
- this is the case in physics – real world is a function, not a vector
- surrogate (for time and space, which can be present)
- is a solution of ODE, is a solution of PDE
- physical prior knowledge: formula for the ODE or PDE
Why is this useful?
- actual simulation may be too expensive (e.g. Schrödinger)
- requires a lot less training data than traditional SBI
Example: growth data (real, not simulated)
TODO: image here
- idea: use physical knowledge as a problem-specific regularizer
- here the growth follows the “logistic rule”:
- we may or may not know (depending on the problem)
- special case of SIR equations – the lecture has a derivation here
- PINN approach to learning:
- two bounds of points (later 3)
- data points TS where is (approximately) known (at least the data for initial condition)
- collocatoin points where we apply the regularizer
- : check if ODE is fulfilled at
- regularization term:
- if fulfilled then it should be zero for any (ideally )
- data term:
- two bounds of points (later 3)
The regression problem is now just
- we do not get a distribution over functions
The lecture talks here about the general case for ODEs.
Benefits of using NNs:
- universal approximators (if big enough) and good convergence in practice
- can in practice learn any
- derivatives easily computable by autodiff
Disadvantages of using NNs:
- for each set of data points and parameters, training must be restarted (no amortization)
- problem is currently addressed (later
Tips and tricks:
- use activation or recently
- standardize the problem (similar to sclaing features to unit variance)
- translate ODE into a “dimensionless” form (use fractions instead of absolutes)
- nice constraint for
- translate ODE into a “dimensionless” form (use fractions instead of absolutes)
- random Fourier features – convert features into the Fourier domain with random projections
- was shown that low-frequency behavior converges much faster than high-frequency
- random weight factorization (replace a linear layer with I don’t know)
PINN-related things (training, variants).
State-of-the-art generative modeling
- our current workhorse are invertible neural networks (affine or spline coupling flows)
- the directions of improvement:
- lift architectural restrictions that only facilitate efficient training
- free-form flows
- potentially higher expressive power (very new)
- opportunity to incorporate application-related architecture restrictions
- allows for bottleneck architectures
- free-form flows
- get higher fidelity of the generated data (image generation, molecular modeling)
- diffusion models
- can generate better data but can’t generate the probability well
- diffusion models
- speed-up generation and inference
- consistency models & injective flows
- lift architectural restrictions that only facilitate efficient training
Free-form flows
- [Draxler, Sorrenson et al. 2023]
- use arbitrary (dimension-preserving) neural networks as encoder and decoder
- e.g. variations of ResNet
- give up invertibility of encoder: by construction
- instead train two separate networks and ensure
- reconstruction loss
- train generative distribution by the maximum likelihood
- express with the change of variables formula
- coupling flows exist to make tractable
- two types of layers in coupling flows
- rotation / permutation layers: for orthonormal
- coupling layers (generally auto-regressive blocks)
- is triangular
- rotation / permutation layers: for orthonormal
- if layer architecture is free, these tricks no longer work must calculate by autodiff
- modern autodiff can do this reasonably but for
- autodiff offers library functions for Jacobian-vector products (
jvp) and vector-Jacobian products (vjp)- can use without actually explicitly constructing the Jacobian
- if is a unit vector, we get a column of
- construct explicitly by
jvpproducts
- construct explicitly by
- fast enough for inference but slow during training – to make it efficient, you do not need – for training, we only need with network parameters
- surprising result: this can be estimated efficiently without access to
The lecture shows the derivation for why this is the case here.
- experiments:
- FFF works as well as other NFs on toy data
- FFF works very well on simple molecular modelling benchmarks
Injective flows
- NF with a bottleneck:
Fever dream.
Bottleneck Free-form Flows
- is linear
- consistency requirement:
- we get is also linear
- infinitely many solutions for if is fixed
- – even worse
- for non-linear pseudo-inverse pairs , ambiguity is even worse
- open problem for higher dimensions
We can formalize the quesiton:
encoder defines equivalence classes of data points mapped to the same code
decoder defines a representative for each fiber
with two constraints:
- , s othat
- if is continuous, is also continuous
even if (and ) are fixed, infinitely many are still possible
- same goes for
how to train an injective free-form flow?
- to use NLL loss, we need a change-of-variables formula
- rectangular/injective c-o-v formula for decoder
- this is a probability on ; says nothing about
need to learn three things:
- manifold that represents well under lossy compression
- fibers which differences between and we choose to ignore
- as distribution of points after projection
much more difficult than NF, which only learn
the squared reconstruction loss
gives reasonable and in practice
- is a kind of average of the original (in lower dimension)
- tend to be orthogonal to (in Euclidean norm)
can be computed by an adapted version of FFF
- training only with (as in standard NF) is impossible (leads to degenerate solutions)
Results: injective FFFs are competitive on standard benchmarks
- scaling it up to serious applications is an open problem
FFFs for data on a known manifold (don’t have to learn it)
- further assume that the projection function is already known
- we also don’t have to learn
- e.g. data are on the surface of the earth (manifold is sphere, projection is orthogonal)
- define only on , not on already has correct topology
- if has finite volume (earth surface area), is a good choice
- trick: train proto-encoder and proto-decoders
- higher expressive power by exploiting large space instead of restricting to
- actual encoder and decoder are defined by projection:
TODO image here
- the FFF trick still works (with a minor modification)
- benefits
- simpler than most competing methods on manifolds
- can be trained by NLL loss
- quite good results on simple benchmarks
- drawbacks
- not quite state of the art
- not tested on real problems