 Bathroom Tile Programming
Bathroom Tile Programming
This post is a follow-up to the video I released on my YouTube channel about bathroom tile programming. It contains a few other problems that didn’t make it into the video (so it wouldn’t be too long), but are interesting to try to solve on your own.
If you have any other interesting problems to share (or you think some of the solutions I have could be improved/are not correct), please let me know 🙂.
Click on tasks to see the solutions.
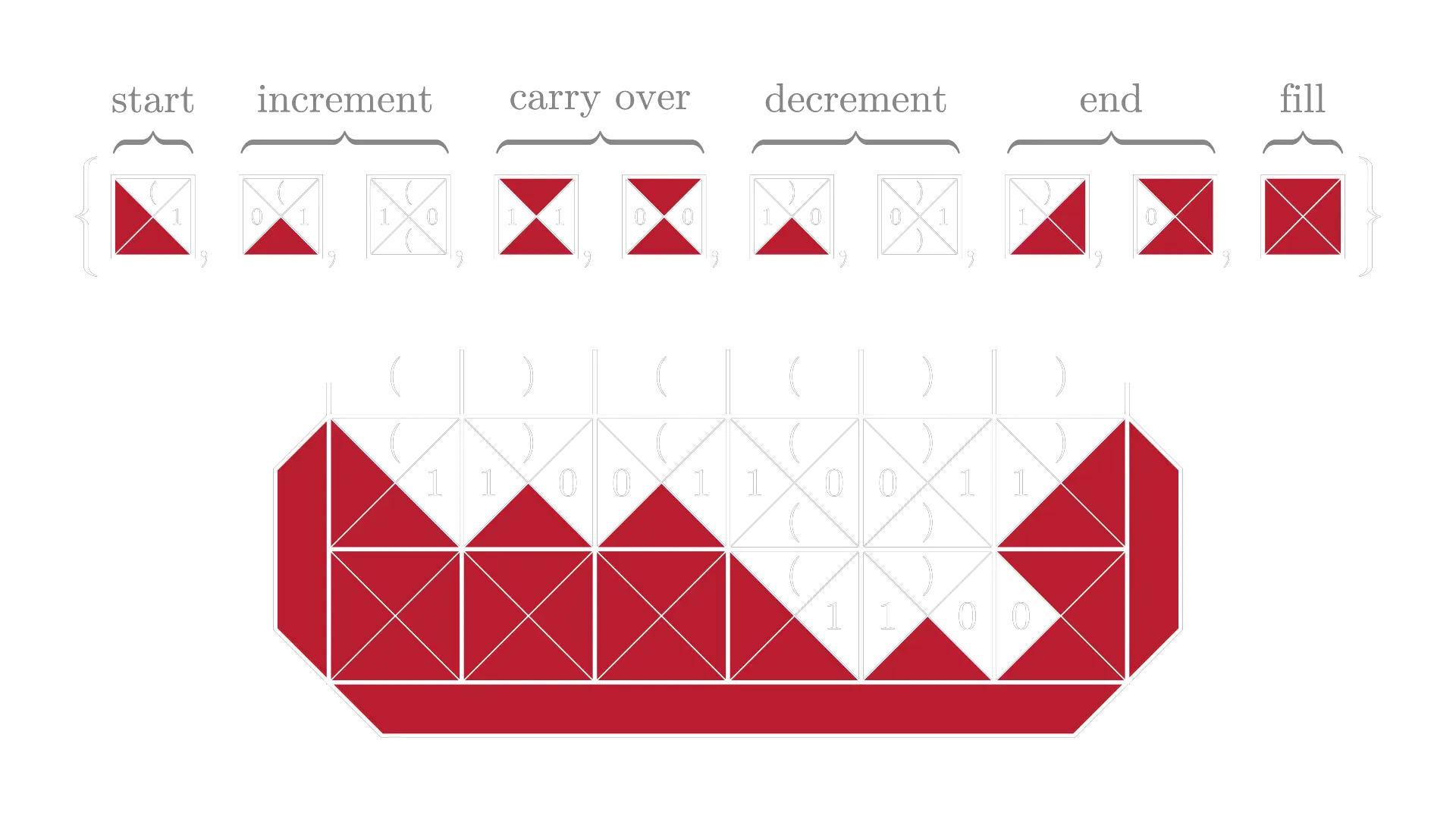
Task: accept the input it contains balanced parentheses
A simple solution that has the time complexity can be found in the video, so this solution concerns only the faster one, which is asymptotically optimal.
The idea is to count, how many parentheses we’ve seen so far and store it in the columns of the tiling as a binary number. When we see a one, we increment – if the previous bit was 0, we put 1 to the right and don’t carry. If it was a 1, we put 0 and do carry (see the diagram above). Same goes for decrementing:
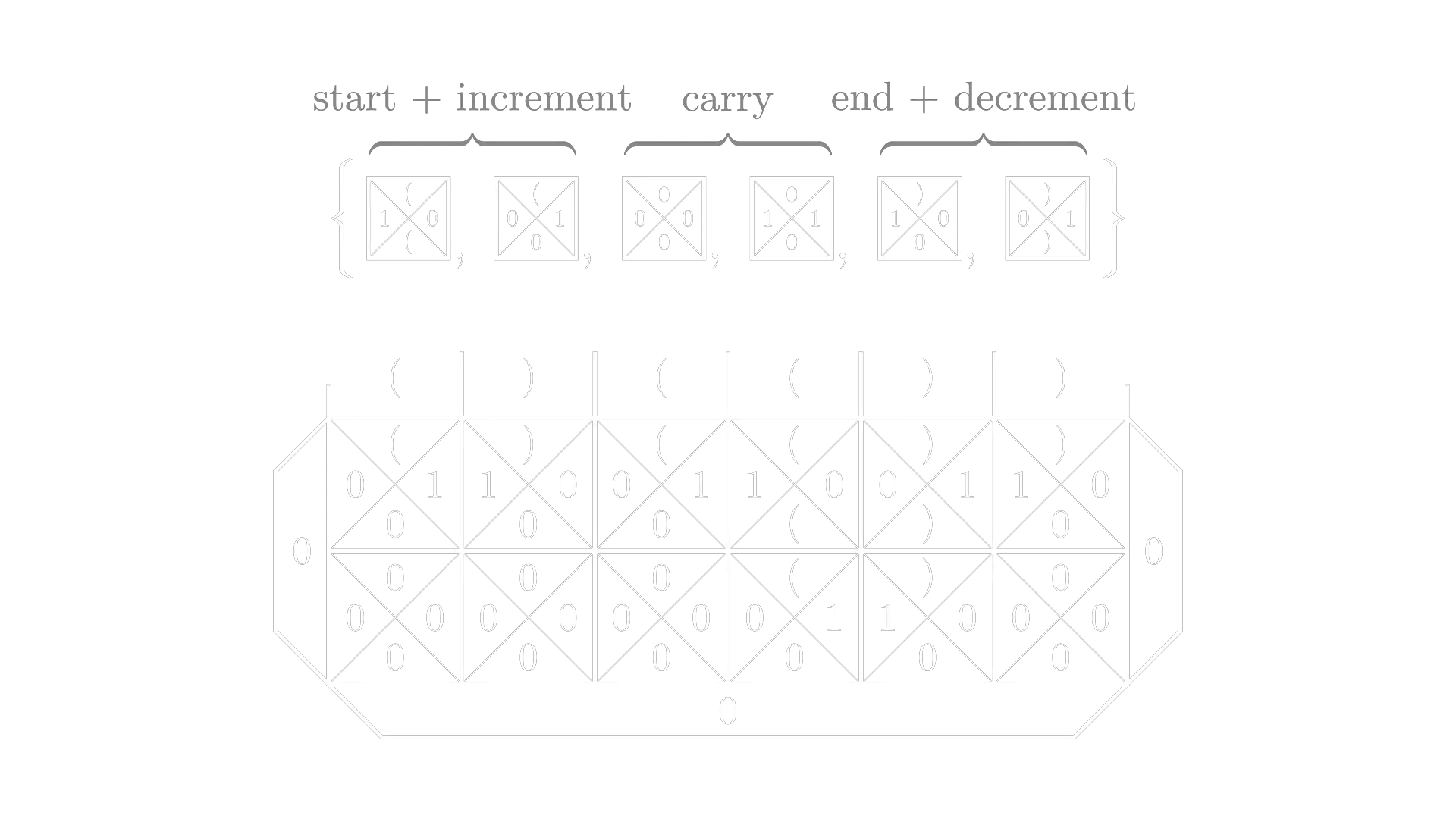
If we wanted to make the tileset a little more concise, we could exchange the color (that is mostly there for clarity) with a zero, yielding the following:
Task: accept the input if contains the same number of zeroes and ones
The solution is very similar to the previous example. We’re again counting in binary. The main difference is that we can go “negative” (since there can sometimes be more zeroes and sometimes more ones), which we handle by counting with two different sets of tiles for positive and negative numbers.
I’m not including the exact solution, since it’s essentially the same as the previous one, only with twice as much tiles.
The time complexity is .
Task: accept the input the number of ones is a power of 2
The main trick here is to realize that numbers in the form are made out of ones in binary, which we can match against the right side of the wall when filling from the left. The only thing we have to figure out is how to subtract one – this we can do with a different left color and a set of tiles that simply ignore the first one on the input and only then start the count.
We also must not forgot to accept a single 1, for which we include a special tile (the last one).
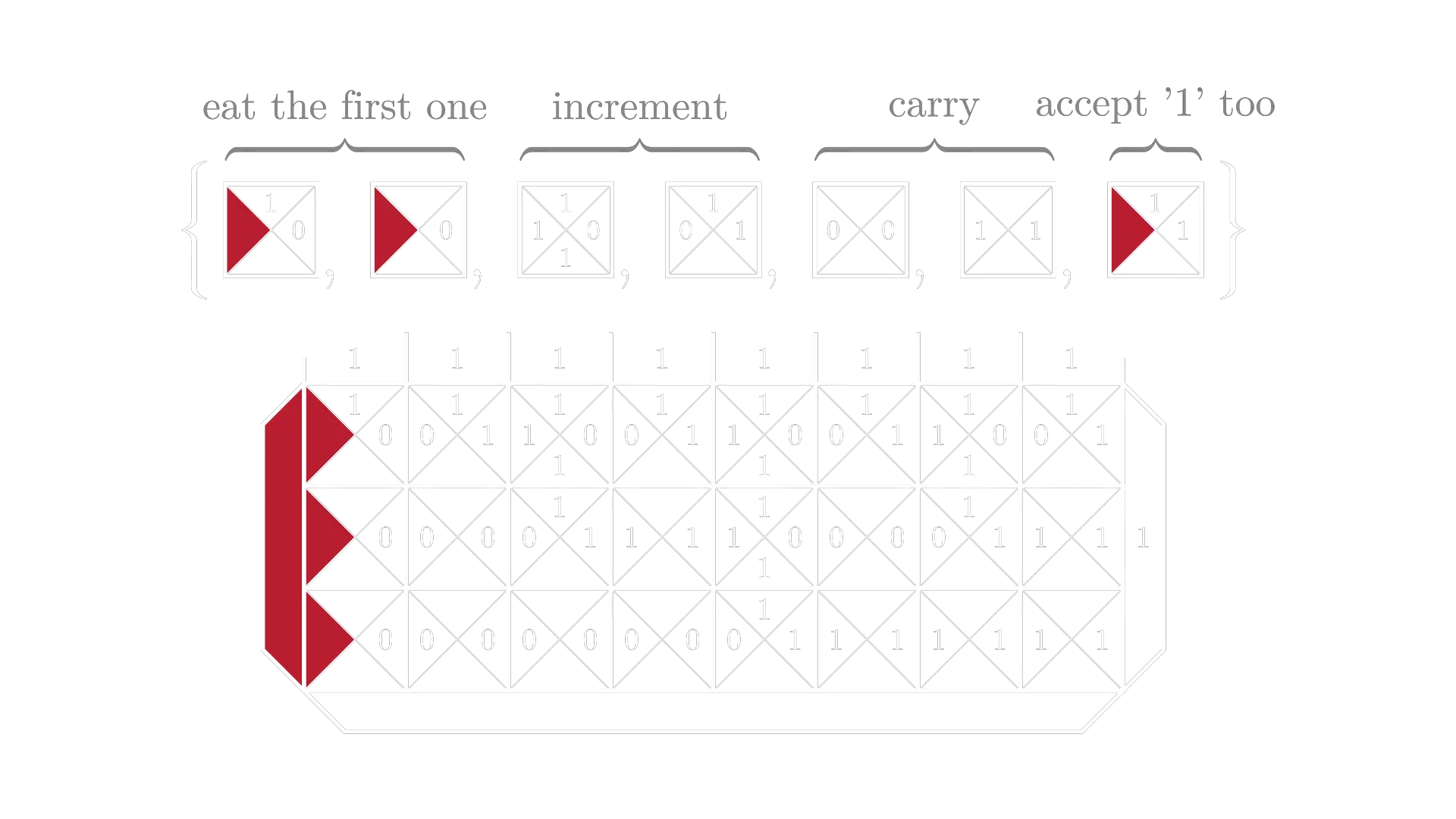
The time complexity is .
Task: accept the input it's a palindrome (of zeroes and ones)
The idea behind the solution is to connect the first and last character and move the rest of the string to the next level. The side colors are there for the odd-size blocks end up in the middle (if the length of the palindrome is odd).
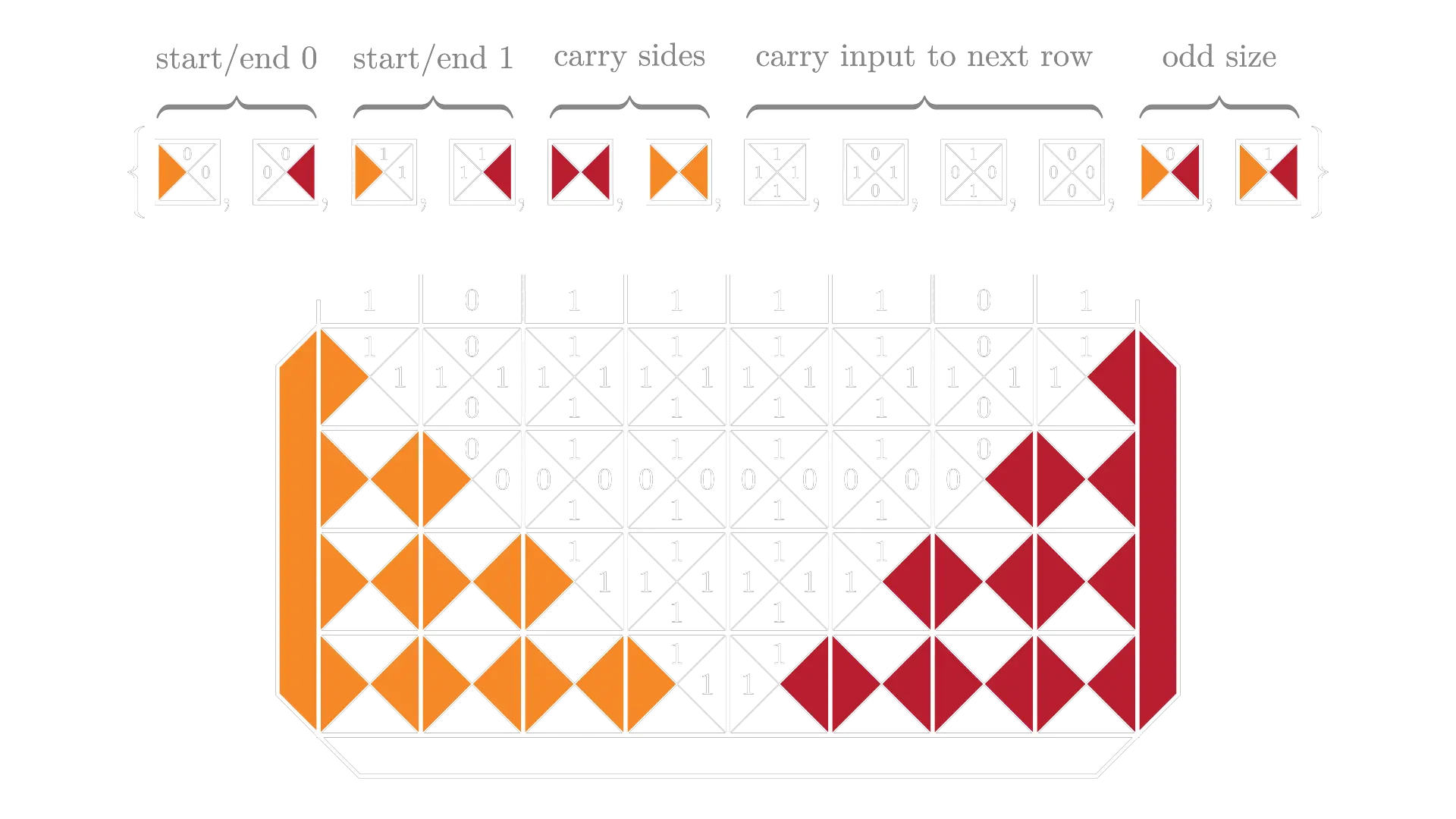
Task: accept the input it is divisible by 13 (given in base 10)
The solution is based on long division, only difference being that we don’t write the result anywhere but simply calculate the remainder. There are a lot of tiles that each correspond to what carry we currently have and what the next input number is.
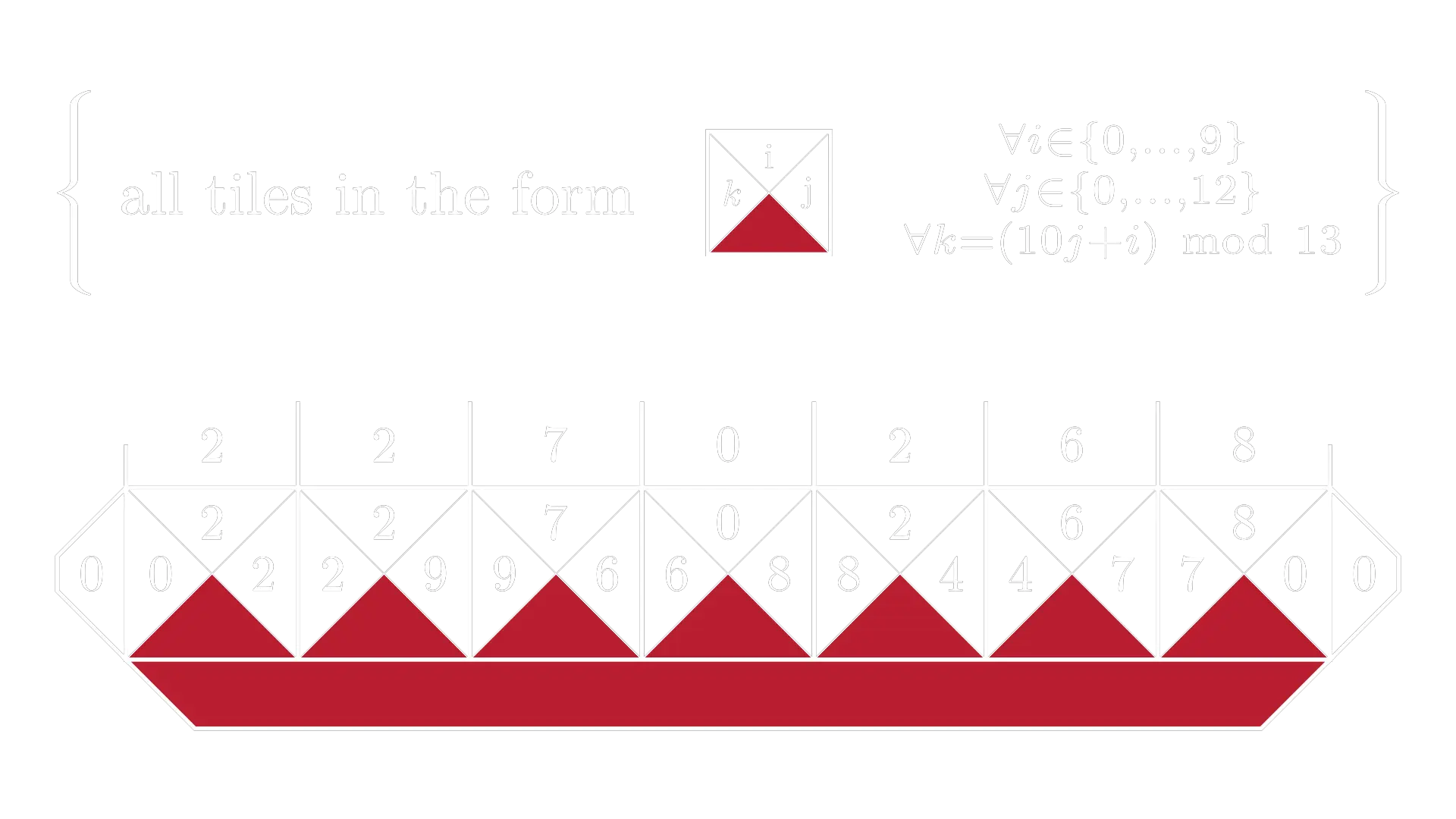
The time complexity is .