 GPU Computing
GPU Computing
- Lecture overview
- Bulk-Synchronous Parallel (BSP) model
- Scaling rules
- CUDA programming
- Thread scheduling
- Optimizing Matrix Multiplication
- Parallelism
- Profiling
- Scheduling optimizations
- -body optimization
- Host-device optimizations
- Productivity
- Stencil computations
- GPU programming models
- Consistency & Coherence
Preface
This website contains my lecture notes from a lecture by Kazem Shekofteh from the academic year 2022/2023 (University of Heidelberg). If you find something incorrect/unclear, or would like to contribute, feel free to submit a pull request (or let me know via email).
Lecture overview
- Introduction [slides]
- CUDA programming [slides]
- Basic architecture [slides]
- Matrix multiplication optimizations [slides]
- Parallel computing [slides]
- Profiling [slides]
- Scheduling optimizations [slides]
- -body optimization [slides]
- Host-device optimizations [slides]
- OpenACC [slides]
- Stencil computations [slides]
- OpenCL [slides]
- Consistency & Coherence [slides]
Bulk-Synchronous Parallel (BSP) model
- established in 1990
- attempt to describe GPU computing
- parallel programs are split into supersteps
- compute something
- communicate what you did
- synchronize with other processors
- parallel slackness: number of virtual processors , physical processors
- : not viable
- : unpromising wrt. optimality
- : leverages slack to schedule and pipeline computation – latency tolerance
Scaling rules
Moore’s law
A law about the exponential increase of processing power, has many variants:
- 1965: number of transistors will double each year,
- 1975: every two years,
- CPU performance will double every 18 months,
- memory size four times every three years, etc.
Amdahl’s law
We want to find the maximum possible improvement, when given
- parallel time of the task, serial time of the task,
- parallel execution units
- best case: linear (if superlinear, something is wrong)
- usually has diminishing returns
CUDA programming
- compute kernel as C program, executed on GPU
- explicit data and thread-level parallelism
- computing, not graphics processing
A program always consists of two parts:
- host = CPU (no/little parallelism)
- device = GPU (high parallelism)
- made up of kernels, which are C functions that are executed on the GPU
- are launched asynchronously (wrt host, not wrt each other)
__global__ void matAdd (float A[N][N], float B[N][N], float C[N][N]) {
// one thread computes one element
int i = blockIdx.x * blockDim.x + threadIdx.x;
int j = blockIdx.y * blockDim.y + threadIdx.y;
// compute only if we're within bounds!
if (i < N && j < N)
C[i][j] = A[i][j] + B[i][j];
}
int main() {
// the thread grid and block structure is 2D, 2D
// adding more/less changes the structure
dim3 dimBlock(16, 16);
dim3 dimGrid((N + dimBlock.x – 1) / dimBlock.x, (N + dimBlock.y – 1) / dimBlock.y);
matAdd <<<dimGrid, dimBlock>>> (A, B, C);
}
Overview
- general kernel syntax is
kernel <<<blockCount, blockSize>>> (args)blockCountandblockSizearedim3and can be 1D/2D/3D
- each thread has a unique
threadIdx.{x,y,z} - each block has
blockIdx.{x,y,z}(andblockDim.{x,y,z}for size)- will be assigned to one streaming multiprocessor
- they are sometimes called Cooperative Thread Arrays (CTAs)
- we have to make sure that the GPU has enough SMs and threads/block to start!
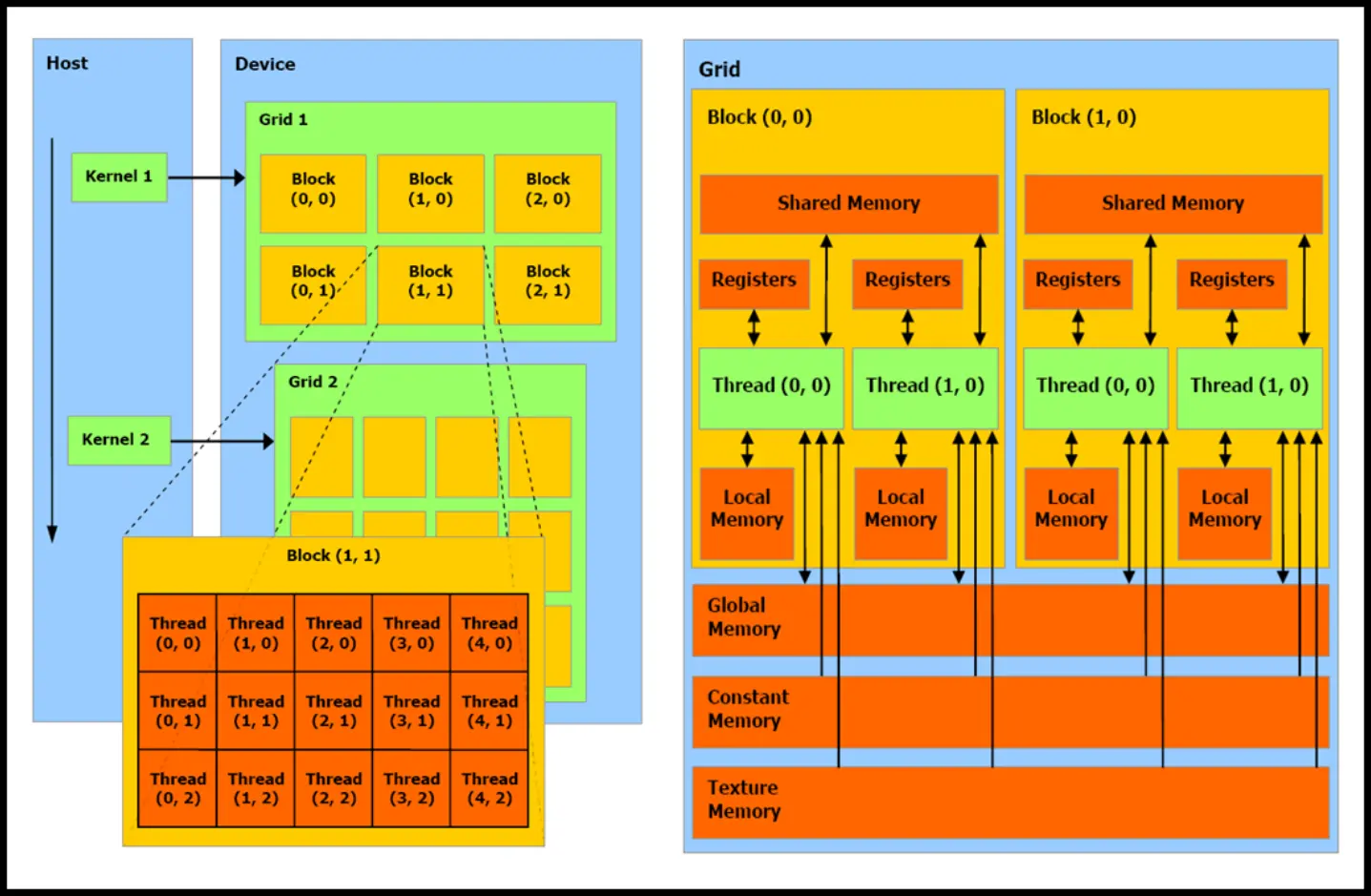
Memory
Global/device memory
- accessible from all threads
- high latency
- lifetime exceeds thread lifetime
- can be quite large, depending on the GPU
- includes thread’s local memory (is only thread-local)
- has address interleaving: successive addresses are mapped to different memory banks so sequential access by multiple threads is faster (each accesses different bank)
- allocation:
cudaMalloc(&dmem, size); - deallocation:
cudaFree(&dmem); - transfer (blocking):
cudaMemcpy(*dest, *src, size, transfer_type);- the
transfer_typeiscudaMemcpy<FROM>To<TO>(Host/Device)
- the
Shared memory
- only accessible from the thread’s block
- access costs is (in the best case) equal to register access
- lifetime is same as thread block lifetime
- can be around for a block (with SM having more to accomodate more blocks)
- organized into banks:
- typically 16-32 banks with 4B width
- parallel access if no conflict (otherwise results in serialization)
- can be static/dynamic, based on if it’s known at compile time or not
- the access time shouldn’t differ (at least not significantly)
// static
__shared__ int s[64];
// dynamic, size is third parameter of kernel call
// extern refers to the fact that it's declared elsewhere (kernel)
extern __shared__ int s[];
Registers
- are at thread level
- depend on run-time configuration
- max. 255 registers/thread
- we can’t really specify what will become a register
- register spilling: if source core exceeds the usage of registers, they spill into local memory
Host memory
- pinned (i.e. can’t be paged out by the system)
- use
cudaMallocHost - is a scarce resource (locks memory out for other processes)
- the OS might limit how much of this can be done
- can be faster if we’re doing a lot of computation on it
- use
- pageable (unpinned)
- just use
malloc
- just use
Code examples
Allocating memory:
float *hMem;
float *dMem;
if (USE_PINNED_MEMORY) {
// casting to (void**) shouldn't be necessary in newer CUDAs
// CUDA's malloc doesn't return the pointer, but a status
// (which in this case is ignored but can be handled)
cudaMallocHost((void**) &hMem, N * sizeof(float));
} else {
hMem = (float*) malloc(N * sizeof(float));
}
cudaMalloc((void**)&dMem, N * sizeof(float));
Copying memory:
// host -> device
cudaMemcpy(dMem, hMem, N * sizeof(float), cudaMemcpyHostToDevice);
// device -> host
cudaMemcpy(hMem, dMem, N * sizeof(float), cudaMemcpyDeviceToHost);
Variable declaration
| Prefix | Location | Access from | Lifetime |
|---|---|---|---|
__device__ |
global memory (device memory) | device/host | program |
__constant__ |
constant memory (device memory) | device/host | program |
__shared__ |
shared memory | device | thread block |
Function declaration
| Prefix | Executed on | Callable from |
|---|---|---|
__device__ |
device | device |
__global__ |
device | host |
__host__ |
host | host |
__global__defines a kernel, return type isvoid__host__and__device__can be combined- for functions executed on the GPU:
- no recursion
- only static variable declarations
- no variable parameter count
Coalescing
Combining fine-grain access by multiple threads into a single operation.
- for global memory, addresses should be multiples of cache line size
- if done improperly, results in significant bandwidth decline:
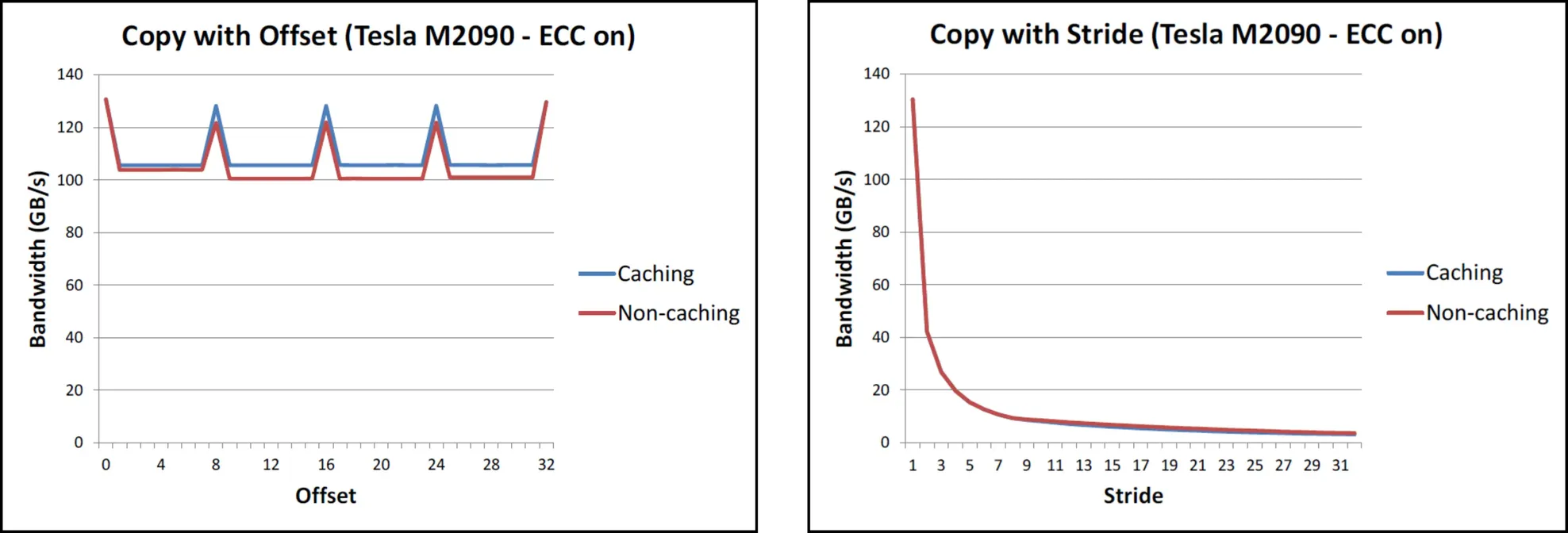
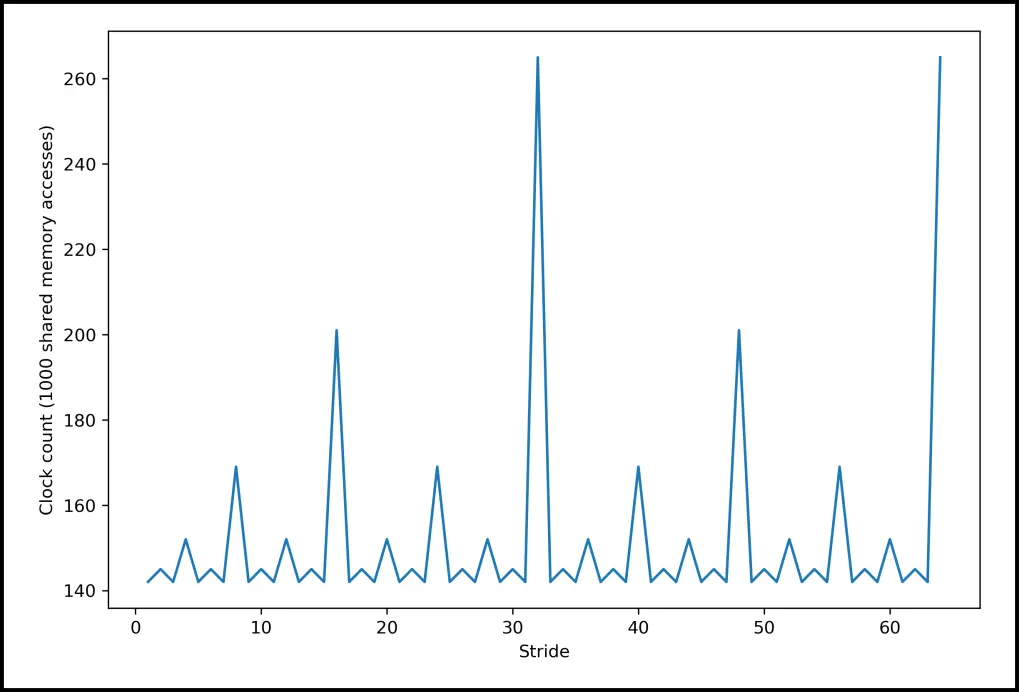
- for shared memory, concurrent access by different threads is handled by the memory banks
- for our cluster, there were banks, where successive mapped to successive banks (mod ), which made the stride pattern look like this:
- thread scheduling does not result in coalesced access, needs to be handled manually!
Thread scheduling
- up to 1k threads per block
- one block executes on one SM (up to )
- no global synchronization! (context switching on GPU is waaaay too expensive)
- threads in a block grouped into warps of (scheduling units of GPU)
- implementation decision, not CUDA
- all threads in a warp execute the same instruction (on their own data and registers)
- for conditionals, a mask is used (all of them still execute the same instruction but only the result of those with the mask are written to the memory)
__global__ badKernel (...) {
id = threadIdx.x;
// not a great idea, use < instead!
if ( id % 32 == 0 )
out = complex_function_call();
else
out = 0;
}
During execution, the hardware schedules blocks to SMs
- happens repeatedly – when some blocks terminate, others will be distributed
- the number depends on a block’s resources (for ex. allocated shared memory)
A SM has multiple warp schedulers that can execute multiple warps concurrently:
- context switching is fast (as opposed to CPU), since the data stays on-chip
- if a warp doesn’t have resources, it is stalled while they are fetched
- this happens really fast because the data stays in registers
- there are multiple policies for scheduling warp executions:
- Round Robin – fetched in a round robin manner
- Least Recently Fetched – fetch based on which has not been fetched the longest
- Fair – fetch for the one with the least amount of fetches
Optimizing Matrix Multiplication
Naive (CPU)
- nothing too interesting, just three loops
- can be further improved by changing the order of addition for better cache hits
__host__ __device__ void GetMatrixValue(int row, int col, float* M, int Width) {
return M[row * Width + col];
}
__host__ __device__ void SetMatrixValue(int row, int col, float* M, int Width, float val) {
M[row * Width + col] = val;
}
void MM_CPU (float* M, float* N, float* P, int Width) {
for (int col = 0; col < Width; ++col) {
for (int row = 0; row < Width; ++row) {
float Pvalue = 0;
for (int k = 0; k < Width; ++k) {
float Melement = GetMatrixValue(row, k, M, Width);
float Nelement = GetMatrixValue(k, col, N, Width);
Pvalue += Melement * Nelement;
}
SetMatrixValue(row, col, P, Width, Pvalue);
}
}
}
Naive (GPU)
- looping handled by a single thread block
- per loop, we do 2 FLOPS and 4 memory accesses
__global__ void MM_NAIVE (float* Md, float* Nd, float* Pd, int Width) {
float Pvalue = 0;
float Melement, Nelement;
int row = threadIdx.y;
int col = threadIdx.x;
for (int k = 0; k < Width; ++k) {
Melement = GetMatrixValue(row, k, Md, Width);
Nelement = GetMatrixValue(k, col, Nd, Width);
Pvalue += Melement * Nelement;
}
SetMatrixValue(row, col, Pd, Width, Pvalue);
}
Multiple thread blocks (GPU)
- we can split the matrix by thread blocks so each thread block does a single index
- no longer limits us to arrays of size (max TPB)
__global__ void MM_MTB (float* Md, float* Nd, float* Pd, int Width) {
float Pvalue = 0;
float Melement, Nelement;
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
for (int k = 0; k < Width; ++k) {
Melement = GetMatrixValue(row, k, Md, Width);
Nelement = GetMatrixValue(k, col, Nd, Width);
Pvalue += Melement * Nelement;
}
SetMatrixValue(row, col, Pd, Width, Pvalue);
}
Using shared memory (GPU)
- we can utilize shared memory to greatly improve the FLOP/global memory access ratio
- then all threads to operation on those
- main trick: copy parts of the matrix from global memory to shared memory!
- creates an additional loop: we tile the blocks such that they fit into shared memory
Note: I think that the code in the presentation is wrong – the tiling doesn’t make sense for sizes other than the size of the block (otherwise threads are writing out of bounds). I’ve modified it, hopefully it’s somewhat correct.
// here we assume that
// - blockDim.x == blockDim.y and they divide Width,
// - nThreads * nBlocks = width ** 2
TILEWIDTH = 32 // same as blockDim.x and blockDim.y!
__global__ void MM_SM (float* Md, float* Nd, float* Pd, int Width) {
// is allocated statically for simpler code
__shared__ float Mds[TILEWIDTH][TILEWIDTH];
__shared__ float Nds[TILEWIDTH][TILEWIDTH];
float Pvalue = 0
int tx = threadIdx.x;
int ty = threadIdx.y;
int row = blockIdx.y * TILEWIDTH + ty;
int col = blockIdx.x * TILEWIDTH + tx;
if (row > Width || col > Width)
return;
// loop over tiles
for (int m = 0; m < Width / TILEWIDTH; ++m) {
// load the tile of both of the arrays
Mds[ty][tx] = GetMatrixValue(row, m * TILEWIDTH + tx, Md, Width);
Nds[ty][tx] = GetMatrixValue(m * TILEWIDTH + ty, col, Nd, Width);
// RAW dependency:
// we must wait for all of them to finish!
__syncthreads();
// do the actual computation
for (int k = 0; k < TILEWIDTH; ++k)
Pvalue += Mds[ty][k] * Nds[k][tx];
// WAR dependency:
// again wait or some threads will change Mds/Nds
__syncthreads ();
}
SetMatrixValue(row, col, Pd, Width, Pvalue);
}
- the
__syncthreads();synchronizes all threads within a single block (“wait here”)- behaves as a barrier to make sure all threads are on the same page
- useful particularly when repeatedly writing/reading shared memory
- RAW (true/data dependency): don’t read before you finish writing
- WAR (anti-dependency): don’t write before you finish reading
- WAW (output dependency): if the last write is important, make sure it’s the last
Parallelism
- sequential program
- single thread of control
- instructions executed sequentially
- concurrent program
- several autonomous sequential threads
- parallel execution possible
- execution determined by implementation
- is not parallelism – we can implement concurrency by interleaving on a single CPU, it just indicates that the threads are independent
Various levels of parallelism:
- Instruction Level Parallelism (ILP) – parallelism of one instruction stream
- huge amount of dependencies and branches
- limited parallelism: pipelining, out-of-order execution
- Thread Level Parallelism (TLP) – parallelism of multiple independent instruction streams
- less amount of dependencies, no limitations due to branches
- limited by the maximum number of concurrently executable streams
- Data Level Parallelism (DLP) – applying one operation on multiple independent elements
- parallelism depends on data structure
- vectorization techniques (single instruction processing multiple values)
- Request Level Parallelism (RLP) – datacenter and customers
The lecture goes into theoretical parallel algorithm design.
Synchronization
Definition (synchronization): enforcement of a defined logical order between events. This establishes a defined time-relation between distinct places, thus defining their behavior in time.
- SIMD (warps on GPU): one instruction, no synchronization necessary
- MIMD: synchronization necessary (shared variables, process synchronization, etc.)
Profiling
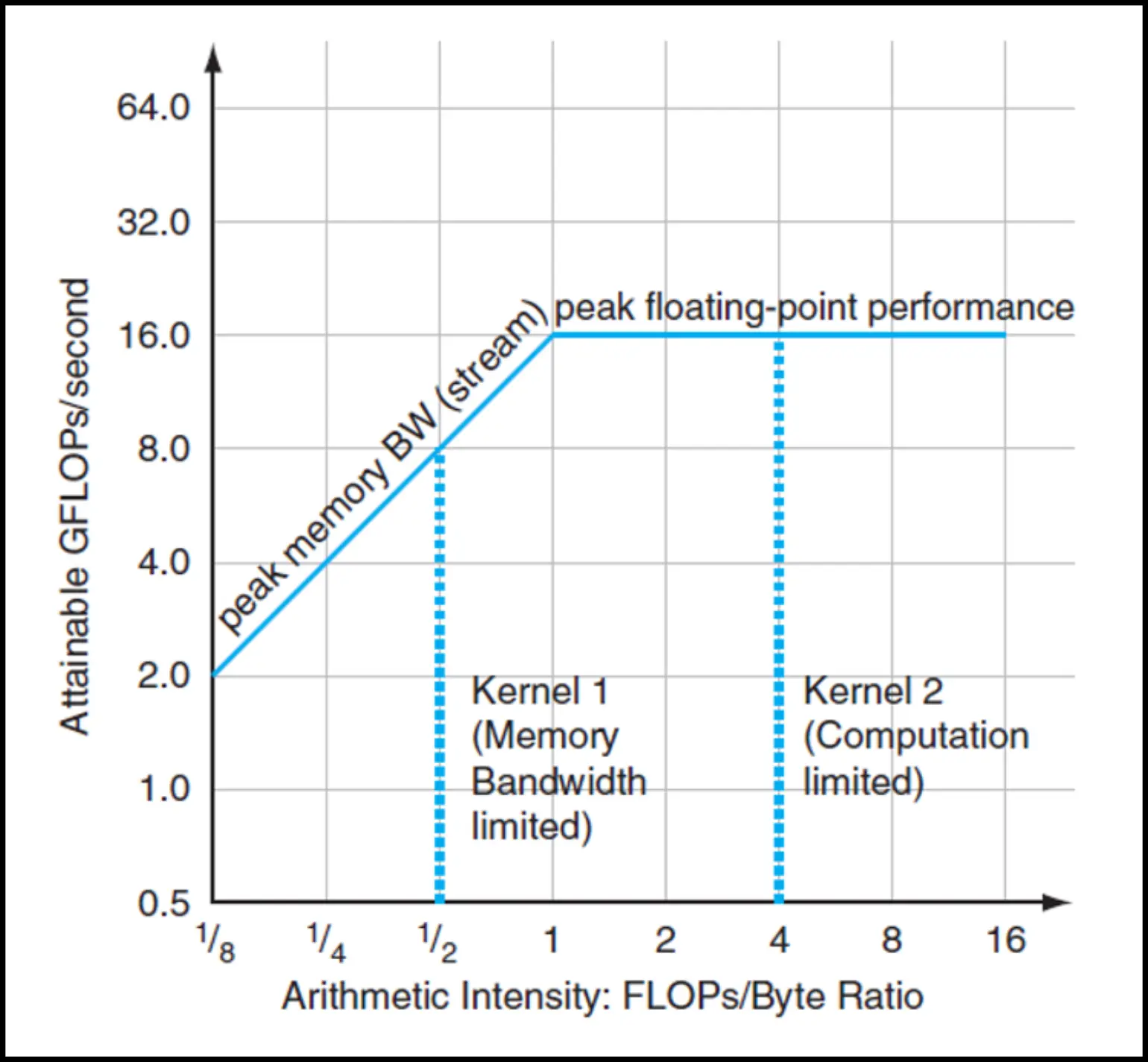
Definition (arithmetic density) , sometimes called computational intensity is the ratio between floating point operations and data movements, i.e.
To evaluate a performance, we use the roofline model:
- the performance is limited by its weakest link – either memory-bound or compute-bound
- obviously depends on the hardware (memory-bound program can become compute-bound when ran on a different machine)
- by optimizing performance, the line can be stretched in both directions
The lecture goes into CUDA profiling. Here are some important concepts:
- Nsight – records and analyzes kernel performance metrics (in detail)
- compute/memory graphs, roofline analysis, etc.
Scheduling optimizations
- common and important data parallel primitive (sum, histogram, etc.)
- easy to implement but hard to implement fast
- to process very large arrays, we will require more than one SM – synchronization problem
- solution: one reduction layer will be one kernel launch
- the examples don’t actually do this, but in practice this would be done
- we’re also assuming associativity (so we can do shenaningans with the order of operations)
Naive implementation
- we’re implementing a reduction add
- one kernel launch will solve a reduction subtree of its block size
- the thread structure is 1D, shared memory stores the subtree
- the output is an array of the results of each block
- this isn’t entirely Naive, we’re already using shared memory
__global__ void Reduction(int *out, int *in, size_t N) {
extern __shared__ int sPartials[];
const int tid = threadIdx.x;
// each thread loads one element from global to shared mem
sPartials[tid] = in[blockIdx.x * blockDim.x + threadIdx.x];
__syncthreads();
// do reduction in shared mem
for (unsigned int s = 1; s < blockDim.x; s *= 2) {
if (tid % ( 2 * s ) == 0)
sPartials[tid] += sPartials[tid + s];
__syncthreads();
}
if (tid == 0)
out[blockIdx.x] = sPartials[0];
}
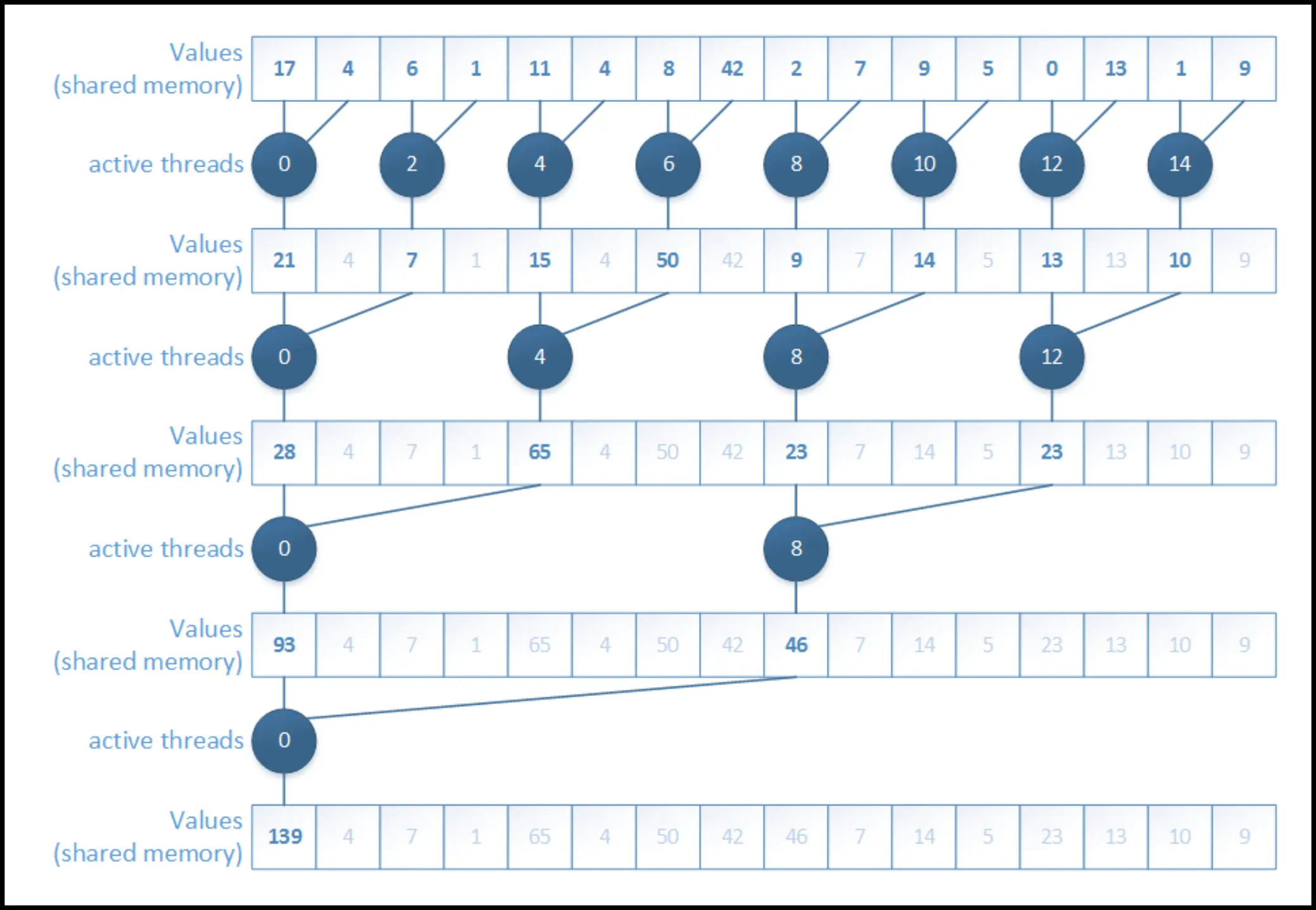
Interleaved address divergent
- remember that all threads in a warp execute the same instructions
- the previous code uses threads from all over the place – let’s use the ones from the start
- improves performance by almost ! (see table below)
for (unsigned int s = 1; s < blockDim.x; s *= 2) {
int index = 2 * s * tid;
if (index < blockDim.x)
sPartials[index] += sPartials[index + s];
__syncthreads();
}
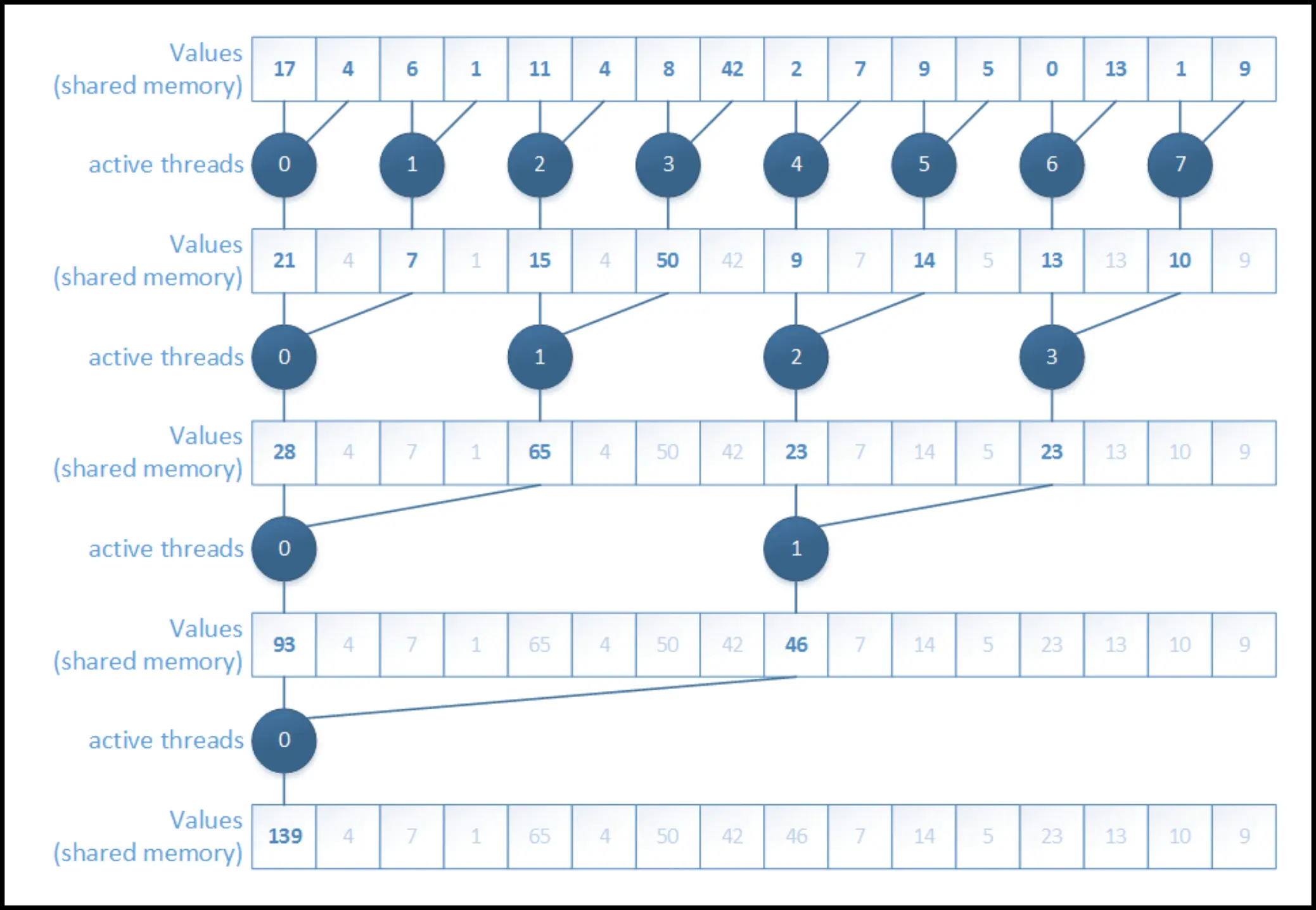
Resolving bank conflicts
- consecutive threads should access consecutive memory addresses
- see memory bank stride access graph from a few sections ago
- another large performance increase (see table below)
- this version seems like the most intuitive one to implement
for (unsigned int s = blockDim.x / 2; s > 0; s >>= 1) {
if (tid < s)
sPartials[tid] += sPartials[tid + s];
__syncthreads();
}
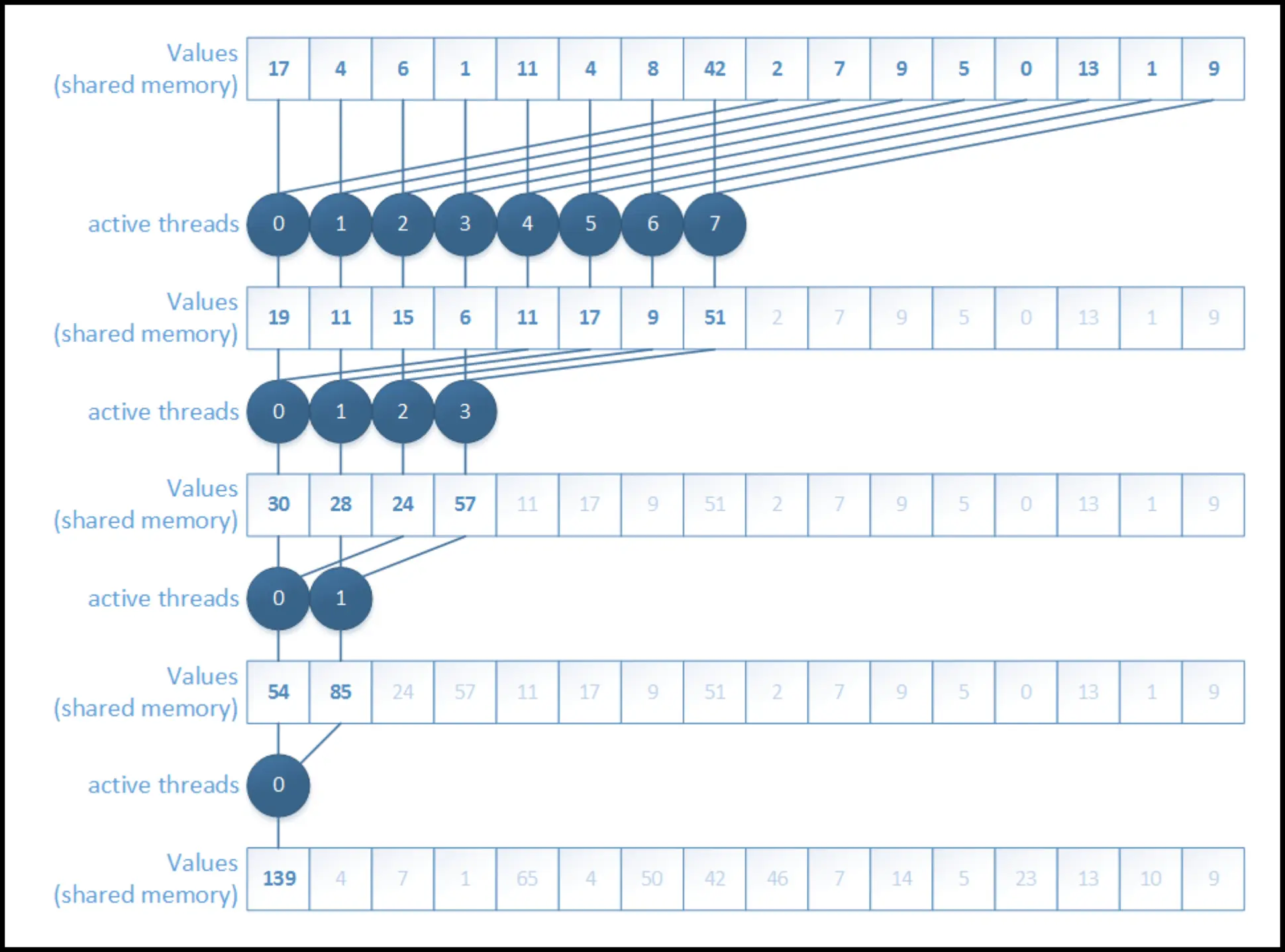
Making use of idle threads
- after the first iteration, half of the blocks don’t do anything
- they just load something to shared memory at the beginning and are done
- idea: start with half of the blocks and do the first operation while loading
- almost double performance increase again!
// we have HALF of the threads but each loads DOUBLE
unsigned int i = blockIdx.x * (blockDim.x * 2) + threadIdx.x;
// each thread loads TWO elements from global to shared mem
sPartials[tid] = in[i] + in[i + blockDim.x];
__syncthreads();
Manual unrolling
- when we have one warp left, we don’t need any
__syncthreads()calls - a bit ugly but functional and further increases the speed
for (unsigned int s = blockDim.x / 2; s > 32; s >>= 1) {
if (tid < 0)
sPartials[tid] += sPartials[tid + s];
__syncthreads();
}
if (tid < 32 && blockDim.x >= 64) sPartials[tid] = sPartials[tid + 32];
if (tid < 16 && blockDim.x >= 32) sPartials[tid] = sPartials[tid + 16];
if (tid < 8 && blockDim.x >= 16) sPartials[tid] = sPartials[tid + 8];
if (tid < 4 && blockDim.x >= 8) sPartials[tid] = sPartials[tid + 4];
if (tid < 2 && blockDim.x >= 4) sPartials[tid] = sPartials[tid + 2];
if (tid < 1 && blockDim.x >= 2) sPartials[tid] = sPartials[tid + 1];
Overview
Here is an overview of the versions we have implemented so far (the values in the table are GB/s for the given version and TPB):
| Version \ TPB | ||||||
|---|---|---|---|---|---|---|
| naive | ||||||
| addresses | ||||||
| banks | ||||||
| first add | ||||||
| unrolling |
-body optimization
- we have bodies and want to evaluate their movement
- uses Newton’s second law of motion
- movement is approximated by temporal discretization (i.e. move by some small time)
I’m not writing the formulas from the slides, this isn’t a physics course.
AOS vs SOA
- AOS: Arrays of Structures
- data grouped per element index, different element types next to each other
- typical in most applications
- consecutive threads won’t access consecutive places in memory
// AOS
struct {
float x, y, z;
float vx, vy, vz;
float mass;
} p_t;
p_t particles [MAX_SIZE];
- SOA: Structures of Arrays
- data grouped per element type, elements distributed among different arrays
- typical in GPU applications (where multiple threads are accessing memory concurrently)
struct {
float x [MAX_SIZE],
y [MAX_SIZE],
z [MAX_SIZE];
float vx [MAX_SIZE],
vy [MAX_SIZE],
vz [MAX_SIZE];
float mass [MAX_SIZE];
} p_t;
p_t particles;
Naive implementation
- single thread takes care of a single body (if blocks cover bodies)
__host__ __device__ void bodyBodyInteraction(...) {
float dx = x1 - x0;
float dy = y1 - y0;
float dz = z1 - z0;
float distSqr = dx*dx + dy*dy + dz*dz;
distSqr += softeningSquared;
float invDist = rsqrtf(distSqr);
float invDistCube = invDist * invDist * invDist;
float s = mass1 * invDistCube;
*fx = dx * s;
*fy = dy * s;
*fz = dz * s;
}
__global__ void ComputeNBodyGravitation_Naive(...) {
// outer loop, in case blocks don't fully cover the bodies
for (int i = blockIdx.x * blockDim.x + threadIdx.x;
i < N;
i += blockDim.x * gridDim.x)
{
float acc[3] = {0};
float4 self = ((float4 *) posMass)[i];
// care: also includes interaction between itself!
// is essentially zero and prevents needless branching
#pragma unroll 16
for (int j = 0; j < N; j++) {
float4 other = ((float4 *) posMass)[j];
float fx, fy, fz;
bodyBodyInteraction(
&fx, &fy, &fz,
self.x, self.y, self.z,
other.x, other.y, other.z, other.w,
softeningSquared
);
acc[0] += fx;
acc[1] += fy;
acc[2] += fz;
}
force[3*i+0] = acc[0];
force[3*i+1] = acc[1];
force[3*i+2] = acc[2];
}
}
#pragma unrollwill reduce branch overhead- the factor has to be determined empirically
- be careful – if isn’t a multiple, might not do some calculations/segfault
Shared memory
- split inner loop into sections (by block width) that are saved to shared memory
- each thread still computes all interactions for one body, but in block-sized chunks
__global__ void ComputeNBodyGravitation_Shared (...) {
extern __shared__ float4 sharedPM[];
for (int i = blockIdx.x * blockDim.x + threadIdx.x;
i < N;
i += blockDim.x * gridDim.x)
{
float acc[3] = {0};
float4 self = ((float4 *) posMass)[i];
#pragma unroll 32
for (int j = 0; j < N; j += blockDim.x) {
// each thread loads its part to the shared memory
sharedPM[threadIdx.x] = ((float4 *) posMass)[j+threadIdx.x];
__syncthreads();
for (size_t k = 0; k < blockDim.x; k++) {
float fx, fy, fz;
float4 other = sharedPM[k];
bodyBodyInteraction(
&fx, &fy, &fz,
self.x, self.y, self.z,
other.x, other.y, other.z, other.w,
softeningSquared
);
acc[0] += fx;
acc[1] += fy;
acc[2] += fz;
}
__syncthreads();
}
force[3*i+0] = acc[0];
force[3*i+1] = acc[1];
force[3*i+2] = acc[2];
}
}
Host-device optimizations
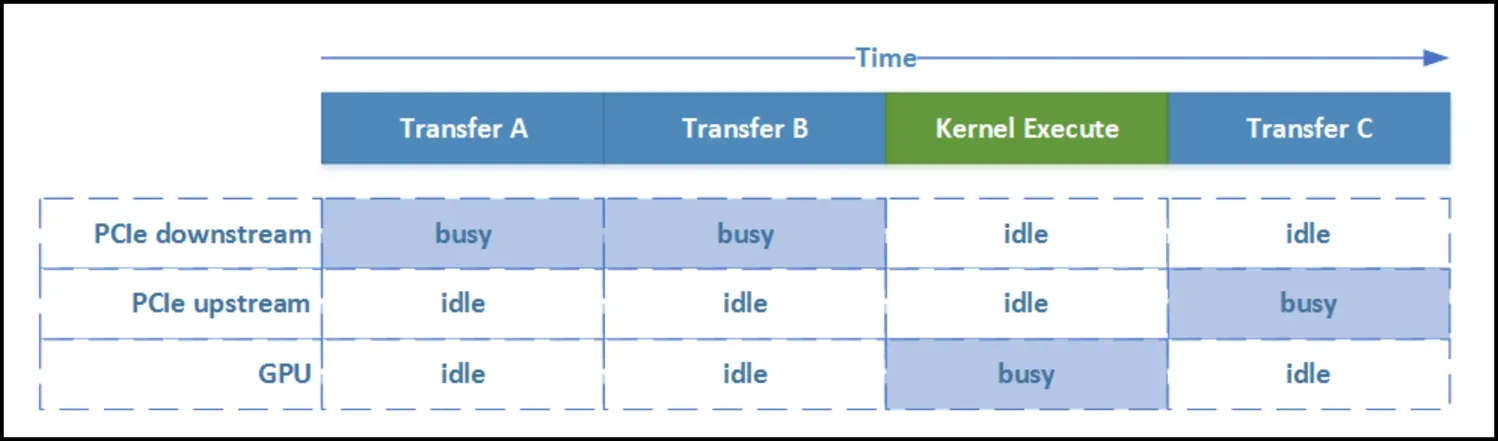
- streams – CPU/GPU concurrency!
- concurrent copy & execute (memcpy & kernel execute)
- here is a nice presentation that sums them well
Host-device synchronization
- context-based – block until all outstanding CUDA operations have completed
cudaMemcpy(),cudaDeviceSynchronize()- all of these operate on the default stream
- is special: will block all other streams until it is finished
- stream-based – block until all outstanding CUDA operations in a stream have completed
cudaStreamSynchronize(stream)– wait until operations on this stream finishcudaDeviceSynchronize(stream)– wait until operations on ALL streams finish- the user specifies which stream a kernel launch/memory operation goes to
kernel <<< ..., cudaStream_t stream >>>cudaMemcpyAsync(..., cudaStream_t stream)
- the number of streams depends on the architecture
- we can also insert events and check when they have been completed
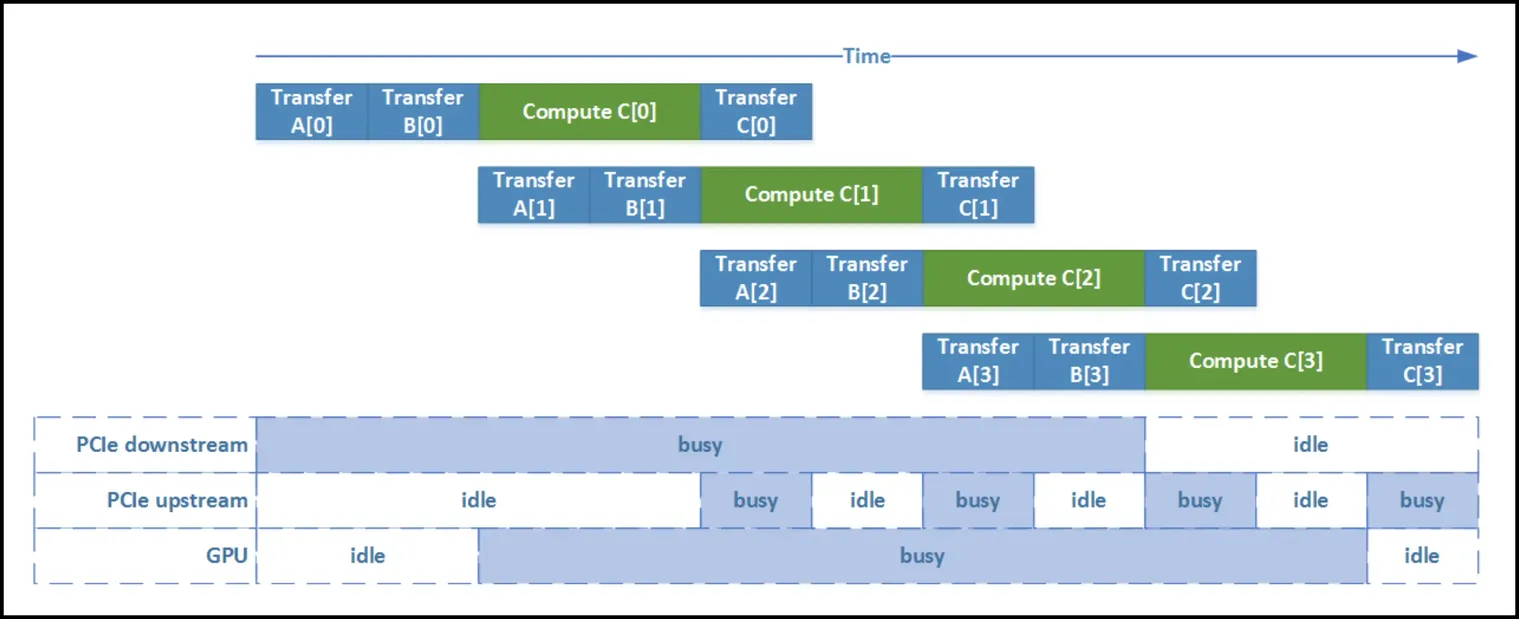
cudaStream_t stream0, stream1;
cudaStreamCreate ( &stream0 );
cudaStreamCreate ( &stream1 );
float *d_A0, *d_B0, *d_C0;
float *d_A1, *d_B1, *d_C1;
// cudaMallocs go here
for (int i = 0; i < n; i += segSize * 2) {
// stream 0
cudaMemCpyAsync ( d_A0, h_A + i, segSize * sizeof(float), ... , stream0 );
cudaMemCpyAsync ( d_B0, h_B + i, segSize * sizeof(float), ... , stream0 );
saxpy <<< segSize/256, 256, 0, stream0 >>> ( ... );
cudaMemCpyAsync ( d_C0, h_C + i, segSize * sizeof(float), ... , stream0 );
// stream 1
cudaMemCpyAsync ( d_A1, h_A + i + segSize, segSize * sizeof(float), ..., stream1 );
cudaMemCpyAsync ( d_B1, h_B + i + segSize, segSize * sizeof(float), ..., stream1 );
saxpy <<< segSize/256, 256, 0, stream1 >>> ( ... );
cudaMemCpyAsync ( d_C1, h_C + i + segSize, segSize * sizeof(float), ..., stream1 );
}
Issues
- hardware used to only have two types of queues:
- copy engine – issues copy operations
- kernel engine – launches kernels
- when the stream is processed, the following happens, resulting in sequential execution
- we have to move the kernel launches after the copies!
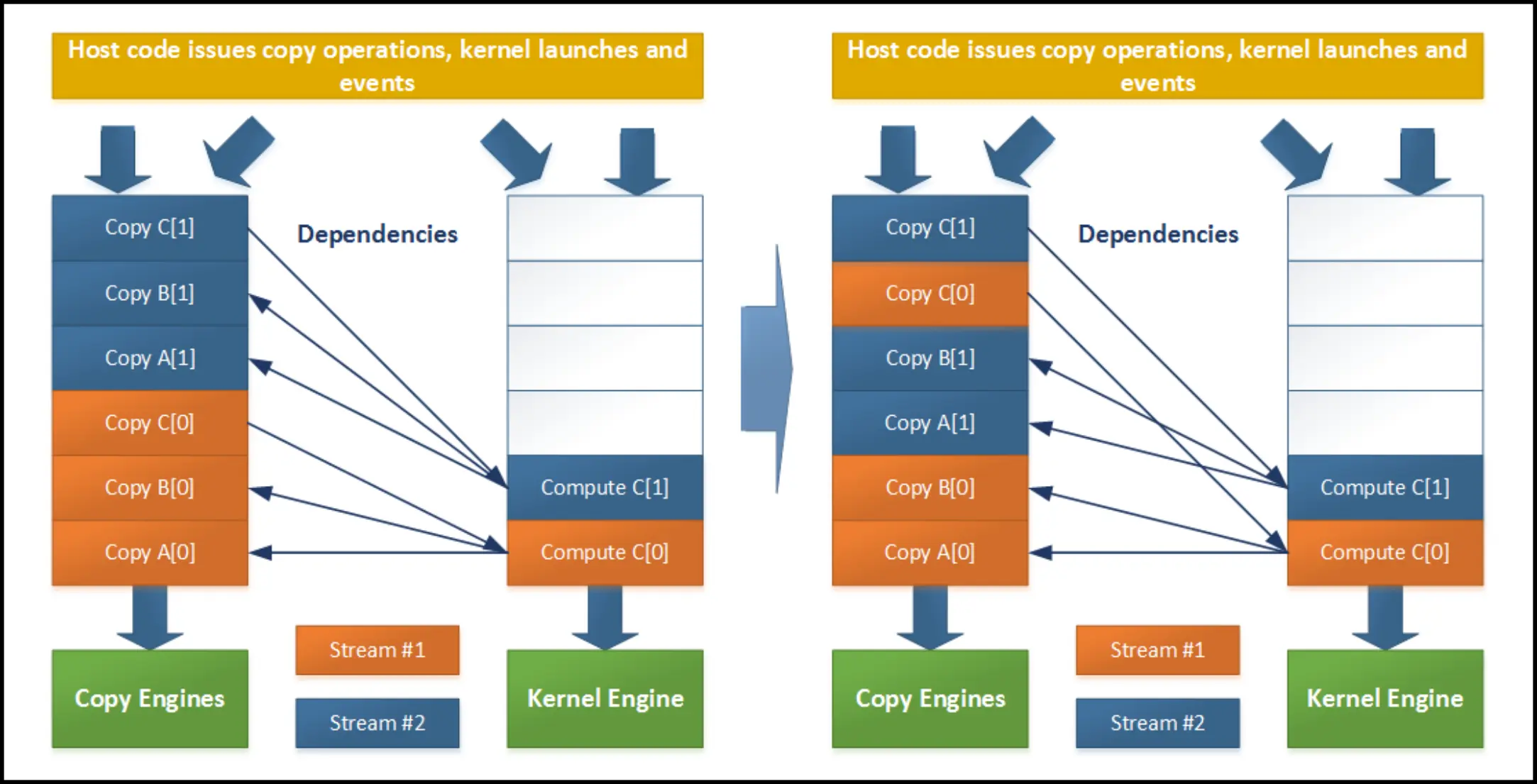
cudaStream_t stream0, stream1;
cudaStreamCreate ( &stream0 );
cudaStreamCreate ( &stream1 );
float *d_A0, *d_B0, *d_C0;
float *d_A1, *d_B1, *d_C1;
// cudaMallocs go here
for (int i = 0; i < n; i += segSize * 2) {
cudaMemCpyAsync ( d_A0, h_A + i, segSize * sizeof(float), ... , stream0 );
cudaMemCpyAsync ( d_B0, h_B + i, segSize * sizeof(float), ... , stream0 );
cudaMemCpyAsync ( d_A1, h_A + i + segSize, segSize * sizeof(float), ..., stream1 );
cudaMemCpyAsync ( d_B1, h_B + i + segSize, segSize * sizeof(float), ..., stream1 );
saxpy <<< segSize/256, 256, 0, stream0 >>> ( ... );
saxpy <<< segSize/256, 256, 0, stream1 >>> ( ... );
cudaMemCpyAsync ( d_C0, h_C + i, segSize * sizeof(float), ... , stream0 );
cudaMemCpyAsync ( d_C1, h_C + i + segSize, segSize * sizeof(float), ..., stream1 );
}
- the newer architectures are better and have multiple hardware queues
- be careful, some operations implicitly synchronize all other CUDA operations
- page locked memory allocation (
cudaMallocHost()orcudaHostAlloc()) - device memory allocation (
cudaMalloc()) - non-async versions of memory operations (
cudaMemcpy(),cudaMemset())
- page locked memory allocation (
Virtual Shared Memory
- lets CPU and GPU have the same address space
- nicer to deal with (only one type of pointers)
-
access costs can be quite significant
- Unified Virtual Addressing (UVA)
- support since CUDA 4
- single virtual address space for all memory in the system
- GPU code can access all memory
- does not automagically migrate data from one physical location to another
- Unified Memory (UM)
- newer way (CUDA 6) of handling memory
- pool of managed memory that is shared between CPU and GPU
- automatic (page) migration between CPU and GPU domains
Productivity
- make compiler responsible for low-level implementations
- generate kernels, launch them
- handle data movements, optimizations
- simplifies the writing process
OpenACC
- directive-based programming model to off-load compute-intensive loops to accelerators
- cross-platform (C, C++, Fortran)
- execution model: host-directed execution with an attached accelerator device
- offloading compute-intensive regions
- coarse-grain parallelism: fully parallel execution across execution units gang parallelism
- limited support for synchronization
- CUDA: grid level
- fine-grain parallelism: multiple threads on a single execution unit worker parallelism
- latency hiding techniques
- CUDA: warps at block level
- SIMD/vector operations: multiple operations per thread vector parallelism
- CUDA: threads at block level
- compiler takes care of memory
- is implemented using directives
#pragma acc directive-name [clauses]parallel– user responsible for finding parallelismskernel– compiler responsible for finding parallelismsloop [clause]– share among threads/execute sequentiallygang– among thread blocksworker– among thread warps of a blockvector– among threadsseq– sequential execution
data [clause]copy– H2D at region start, D2H at region endcopyin/copyout– in/out devicecreate– device allocationpresent– note that the data is already there
- is an iterative process (test, see how it does, repeat)
Naive version
int main() {
int n = 256*1024*1024; float a = 2.0f; float b = 3.0f;
float* x;
float* y;
// allocate & initialize x, y
for (int i = 0; i < n; ++i)
y[i] = a*x[i] + y[i];
for (int i = 0; i < n; ++i)
y[i] = b*x[i] + y[i];
//free and cleanup
}
kernels pragma
- the compiler will let us now what it did
- which kernels it launched
- what it copied
int main() {
int n = 256*1024*1024; float a = 2.0f; float b = 3.0f;
// restrict states that the memory of the pointers doesn't overlap
// is useful for compiler optimizations
float* restrict x;
float* restrict y;
// allocate & initialize x, y
#pragma acc kernels
{
for (int i = 0; i < n; ++i)
y[i] = a*x[i] + y[i];
for (int i = 0; i < n; ++i)
y[i] = b*x[i] + y[i];
}
//free and cleanup
}
parallel loop pragma
- “please, distribute this loop over different threads”
int main() {
int n = 256*1024*1024; float a = 2.0f; float b = 3.0f;
float* restrict x;
float* restrict y;
// allocate & initialize x, y
#pragma acc parallel loop
for (int i = 0; i < n; ++i)
y[i] = a*x[i] + y[i];
#pragma acc parallel loop
for (int i = 0; i < n; ++i)
y[i] = b*x[i] + y[i];
//free and cleanup
}
data pragma
- “please, copy this data to the accelerator”
- “now distribute this for loop, oh and also you have the data already”
int main() {
int n = 256*1024*1024; float a = 2.0f; float b = 3.0f;
float* restrict x;
float* restrict y;
// allocate & initialize x, y
#pragma acc data copyin(x[0:n]) copy(y[0:n])
{
#pragma acc parallel loop present(x,y)
for (int i = 0; i < n; ++i)
y[i] = a*x[i] + y[i];
#pragma acc parallel loop present(x,y)
for (int i = 0; i < n; ++i)
y[i] = b*x[i] + y[i];
}
//free and cleanup
}
Nested loops
// distributes outer loop to n threads
// each thread executes the inner loop sequentially
// block size 256, block count n/256 (rounded up)
#pragma acc parallel vector_length(256)
#pragma acc loop gang vector
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < m; ++j ) {
// do stuff
}
}
// same as above but only 16 blocks
// some threads might have to loop multiple times
#pragma acc parallel vector_length(256) num_gangs(16)
#pragma acc loop gang vector
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < m; ++j ) {
// do stuff
}
}
// parallelizes both loops
// distributes n outer loops to n blocks
// distributes inner loop to their threads (256/block)
#pragma acc parallel vector_length(256)
#pragma acc loop gang
for ( int i = 0; i < n; ++i ) {
#pragma acc loop vector
for ( int j = 0; j < m; ++j ) {
// do stuff
}
}
Stencil computations
- iterative kernel that updates regular arrays based on certain patterns
- useful for image processing, partial differential equations, fluid dynamics, etc.
Image processing
- connected component labeling – identify connected areas in this image
- each segment will be labeled with a different value
- -way or -way connectivity (we do )
- for an image, we apply a threshold to create a black/white image
Note: I am beyond confused to what the algorithm actually is, this is my best guess:
- parallelly set labels to the entire stencil (taking threshold into account)
- parallelly (repeatedly) merge labels (taking the minimum)
- will be done diagonally
- wavefronts – storing previous elements in shared memory to reduce memory contention
Partial differential equations
Read the slides, I’m fairly certain this isn’t too important.
Performance optimizations
- stencil codes are memory-bound
- when partitioning the data, there is overlap (called the halo)
- vertical halos are poorly aligned in memory
- marching planes – only keep 3 planes in shared memory, cycling the buffers
GPU programming models
- up to now, we’ve seen CUDA
- similar approach: OpenCL (imperative language)
- directive-based: OpenACC (declarative language, we’ve seen it)
OpenCL
Platform model
- host stays host
- compute devices are things like GPUs
- contain compute units (SMs), which have processing elements (thread blocks/warps)
Execution model
- host code (sequential parts, control)
- kernels still run on device (computational intensive part)
- context – devices, kernel objects, program objects, memory objects
- we have to explicitly create queues for different types of commands
- work item – kernel function in execution for a single point in the defined index space
- global ID / work group ID + local ID
- work group – organization structure of work items with a given kernel instance
- synchronization between work groups not possible (same as CUDA)
- can synchronize between work items
NDRange: -dimensional index space
| CUDA | OpenCL |
|---|---|
| Grid | NDRange |
| Thread Block | Work group |
| Thread | Work item |
| Thread ID | Global ID |
| Block index | Block ID |
| Thread index | Local ID |
Different types of kernels exist:
- OpenCL kernels: kernel objects associated with kernel functions (user kernels)
- Native kernels: execution along with OpenCL kernels on a device and shared memory objects
- Built-in kernels: specific for a particular device
Memory model
- memory regions: distinct memories visible to both host and device
- memory objects: objects defined by the OpenCL API
- Shared Virtual Memory: virtual address space exposed to both host and devices (UM in CUDA)
- has special memory objects: buffer, image, pipe
| CUDA | OpenCL |
|---|---|
| Host memory | Host memory |
| Global/device memory | Global memory |
| Shared memory | Local memory |
| Registers/local memory | Private memory |
Consistency & Coherence
Ordering problem: threads operate independently: which order to apply?
Cache coherence: two threads write to same variable, which gets written to cache:
- caches have to be coherent (all threads see the same value)
- different cache policies:
- write-back: write to cache, at some later point write to memory
- write-through write to cache and immediately to memory too
- both cases have coherence problems, if we don’t update caches of other threads
- a microarchitectural feature
Memory consistency: the order in which memory operations appear to be performed
- as opposed to coherence, focuses on the order of execution
- strict: any write seen immediately
- sequential: write by different processors needs to be seen in teh same order by all processors
- highly relaxed for GPU, few guarantees
__threadfence()stalls current thread until all writes to shared/global memory are visible to other threads (if_threadfence_block()then only shared memory)__syncthreads()is a stronger version since it also synchronizes thread execution
- an architectural feature